0

So I've seen different reasonings for this; which is correct, or are they both corollaries of each other?

1) For a particle to be at rest, we would know its momentum and therefore by Heisenberg's uncertainty principle, the uncertainty in its position would be infinite. Is this acceptable?

2) $\lambda = h / p = h / 0 \implies \lambda \rightarrow \infty$ which is not possible.

EDIT:

Another reason:

3) Due to the zero-point energy, even in its ground state there will always be non-zero kinetic energy.

Keir Simmons
  • 133

2 Answers2

1

Let us take an electron's track in a bubble chamber where there is also a magnetic field.

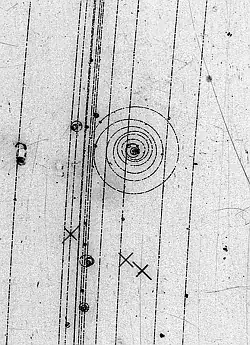
electron track

We can measure the momentum of the electron, the change due to ionisation, and its position as it goes through the spiral and finally know its final (x,y,z) at rest, and 0 momentum.

Even though we are dealing with an elementary particle we are still, with our measurements and the errors in position and momentum at the realm where the Heisenberg Uncertainty Principle is obeyed just by the magnitude of measurement errors.

Now suppose we had a detector at the level of individual hydrogen atoms . One of them has captured this specific electron. The bound electron fulfills the Heisenberg uncertainty principle (HUP) as it is expressed as a solution of Schroedinger's equation. On the other hand there are no infinities, just indeterminacy and a probabilistic value for momentum of the electron in the orbital. It is never at rest around the atom

With this answer I am trying to stress that at the level of nanometers and below, the atomic and molecular dimensions, the concept of "at rest" is a classical concept that has no meaning in a quantum mechanical system. The classical framework has to be abandoned once the dimensions and momenta are constrained by the HUP. The electrons, for example,will be in some quantum mechanical orbital, whether atomic or band structure . They are not "free" except in a vacuum and there the only way we can know of their existence will be by electric and magnetic fields where again the HUP will be the constraint , and when momenta will be so low as to be called "at rest" the electron will be in an energy level of the magnetic or electric field that is sensing it. So the quantum mechanical level with the HUP does not allow/smooths infinities.

Community
  • 1
anna v
  • 236,935
0

The second statement somehow depends on the context, but in the situation that you have in mind they are equivalent, I would say.

According to the uncertainty principle the particle at rest is everywhere in space simultaneously, as you say.

With the second statement you have to be a bit more careful, because the relation you state is in a strict sense a relation for a plane-wave wave-packet. If you want to describe the particle by a wave function you have to consider that the wave function in space is just the Fourier transform of the momentum wave-function, which is a delta distribution. This Fourier transform is then a constant function, which agrees with the statement 1). The assignment of a wave-length to a constant function is not really meaningful.

André
  • 310