This answer gives a great explanation of why the field inside a wire connected to a battery must be equal at all points: Why doesn't the electric field inside a wire in a circuit fall off with distance from the battery?
The answer uses the concept of surface charge buildup to show why the field has to be equal at all points and why it must be perpendicular to the wire.
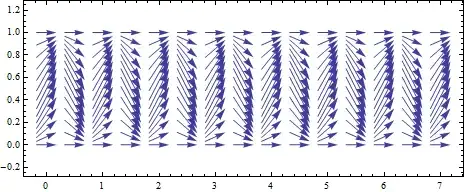
However, there are a lot of ways a field could exist in a wire that is not perpendicular to the wire, but would not cause surface charge buildup:
For example these fields:
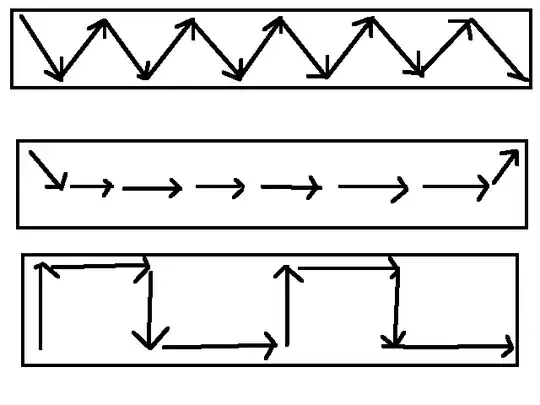
could exist instead of:
and there would still be no surface charge build up.
So my questions are:
Can these "exotic" fields exist"?
If not, why not?
If these exotic field exist, how would current be defined in the wire? Since the electrons are not flowing perpendicular to the wire, would current be defined as the component of the movement of the electrons perpendicular to the wire or just the entire movement of the electrons?
The image below is a resistor. The "lines" represent the current direction and density ("the current density streamlines") . The "gray objects" represent wires through which a voltage difference is applied. If the electric field is always parallel to the surface how can the current lines be at an angle in the first resistor?
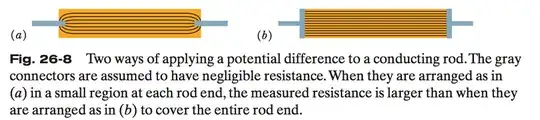
**
Please address all my questions separately. Thank you.
**