4

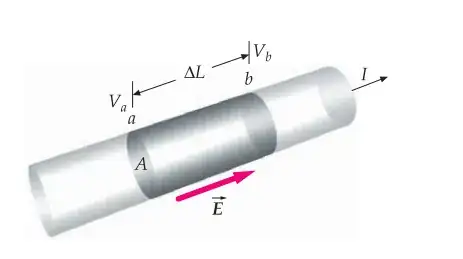
Introduction: Resistance for a uniform cylindrical$^1$ thing in which "field is uniform and along the cylinder" (this can be equivalently replaced by "the same potential difference is constant across any point on one end any point on other") such that $I$ current flows through its CSA is defined as $R=\frac{\Delta V}{I}^{*},$ where $\Delta V$ is the potential difference between the ends of the cylinder.

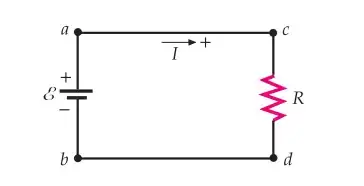
enter image description here

Now consider the circuit. What is the potential difference across the resistor? You may say it is $\epsilon= \Delta V=IR.$

enter image description here enter image description here

But how can you be sure? In answering it you assumed that

  1. The resistor is made of circular wire.
  2. You also assumed that the electric field in it is uniform.
  3. And that the direction of the field is along the wire.

The first is justified by that the books assume that the resistor is of CCR type. The second and third are bugging me.

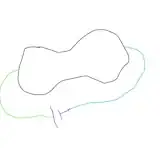
Questions: The question is what short of field does a battery create inside a wire and anything at all in general? If a conductor of any shape, say bone-shaped, is connected to a battery via wires what short of the field will be produced (see $3^{rd}$ image)?

$1:$ Using integral calculus you can calculate resistance for any substance from this definition.

$*$: This is the definition of resistance and not Ohms Law. The law states that for such cylinder we have $\vec{E}=\rho \vec{J}$ where $\rho$ is constant for the type of material and $\vec{J}$ is current density, from this we derive that $R$ is constant for the particular object.

Clemens Bartholdy
  • 8,309
Osmium
  • 540

2 Answers2

1

What is the potential difference across the resistor? You may say it is ϵ=ΔV=IR.

But how can you be sure? In answering it you assumed that

The resistor is made of circular wire. You also assumed that the electric field in it is uniform. And that the direction of the field is along the wire.

Actually, none of those assumptions are made. We simply measure the current through the device and the voltage across the device. If the resulting current-voltage relationship is that $V \propto I$ then we call the device a resistor and the constant of proportionality the resistance.

From a circuit theory perspective the device itself is a complete black-box. We don't care or even know how that current-voltage relationship occurs, the internal details are irrelevant. Circuit theory simply takes that relationship as a given and uses it.

The assumptions of circular cross-section, uniform E field, and E field parallel to the wire are only used in a simple derivation of the physical basis of resistance. They are used only to simplify the problem so that introductory students can do the derivation. They are not in any way necessary conditions for resistance or resistors. Circuit theory simply doesn't care about those details, and all of those assumptions could be violated in a resistor. Such a non-standard resistor would be difficult for a student to derive the resistance, but it would still function just fine.

Dale
  • 117,350
1

A battery pulls electrons from the positive terminal and puts them on the negative terminal. The charge then distributes itself throughout the external circuit so that the line integral of the electric field from one terminal to the other (the potential difference) is the same for any path taken through the circuit. For a uniform length of wire with continuity of current flow, the existance of a uniform field requires a uniform rate of change in the charge per unit length.

R.W. Bird
  • 12,280