Can someone in a simple way explain me what the Fermi level is and what does it have to do with conductivity. My teacher said that Cu conducts electric current better than Al because of something in relation to Fermi level, I didn't get him very well, so please explain me what it is all about, but in a simple way.
2 Answers
Fermi energy
If you operate at zero temperature, $T = 0$ K and fill the energy-states of a system according to the Pauli-exclusion-principle, the Fermi energy is the boundary at which all lower states are full and all higher states are empty. At $T = 0$ this boundary is a sharp line.
For example, say you have ladder with five steps which you have to “fill” with ten electrons. Due to the Pauli-exclusion principle, each step can only take two electrons. Now you fill up the ladder: 2 electrons in the first step, the next two in the second step and so forth until you put the last two electrons in the 5th step. The energy at this step (the 5th step) is your Fermi energy.
Metals have Fermi energies of several electron-volts (eVs). (Cu: 7 eV, Al: 11 eV) For comparison, the thermal energy at room temperature is about $k_B T \sim $ 0.025 eV.
Connection to the conductivity
First you must know that only electrons with an energy close to the Fermi energy can participate to the conduction process. Why? I mentioned earlier that at $T = 0$, the Fermi energy is a sharp line. At $T > 0$, this sharp line gets “washed out” and you get something like this:
$\hspace{1.8in}$
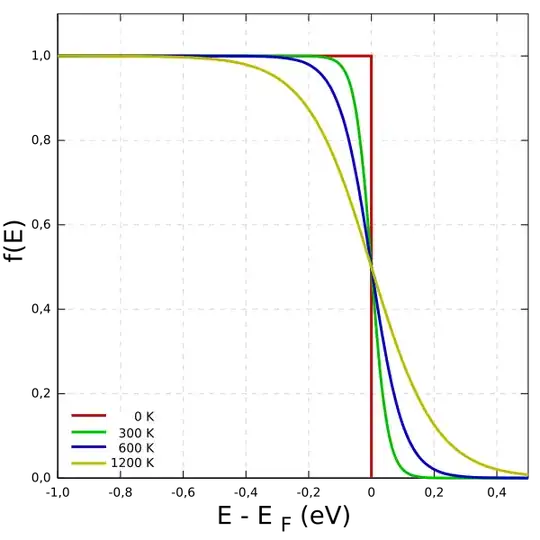
This means that instead of only full and empty states, you now have half empty states above and below the Fermi energy. This is turn means that you are now able to excite electrons in higher energy states, which you need to do if you want to accelerate them in a direction; i.e., if you want to do work on them.
But in consequence of the small contributions of the thermal and electric energies (thermal $ \sim $ 0.025 eV, electric less than that), you are only able to excite electrons VERY CLOSE to the Fermi energy ($E_F$). So only electrons close to $E_F$ will contribute to the conduction.
With this $E_F$ you can associate a velocity, the Fermi velocity: $$ v_F = \sqrt{2 E_F / m} $$
Now let's turn to the conductivity:
The conductivity $\sigma$ is defined as $$ \sigma = \frac{n e^2 \tau}{m} $$ where $n$ is the number of electrons, $e$ is the electron charge, $\tau$ is the time between two collisions and $m$ is the mass of an electron.
One can obtain $\tau$ from $\mathscr{l}$, the mean free path between two collisions, given as $\mathscr{l} = v_F \tau$ or inversely, $\tau = \mathscr{l}/v_F$. During this time, the electron is accelerated. A LARGE $v_F$ will therefore result in a SHORT acceleration time and LESS gain of speed for the electron in a given direction.
Finally you can write the conductivity as: $$ \sigma = \frac{n e^2 \mathscr{l}}{m v_F} $$
Remember that $v_F$, the Fermi velocity, is directly related to the Fermi Energy $E_F$.
As an instance, consider this table of Fermi energies: Copper has a LOWER Fermi energy (7 eV) than aluminum (11 eV), so it has a LOWER Fermi velocity; hence, the time between two collisions ($\tau$) is LONGER than that in aluminum. This in turn means that the electron has MORE time to accelerate in a given direction which finally explains why copper is a better conductor.
- 137,480
I suppose it depends upon how you define "simple," but in my opinion the best answer is no; explaining thousands of pages from books about QM, solid state physics, electronics, rheology, etc. "in a simple way" as the question requires implies these works could be reduced to a few pages, which would seem unlikely at face value.
Gregor Michalicek has argued (see comments below) that one should overlook this issue, and answer a different version of the question in which the simple clause was removed. I disagree. I think there are many examples in history of science when bad science was done because people glossed over issues or ignored implied or hidden assumptions in their research.
At any rate, my answer of "no" being the best answer is probably impossible to prove. But, to attempt to make my case, what I am going to do is see if the other answer here is both correct and simple. If I am right, it will either be wrong or not simple.
As a preliminary remark, the other answer here by NoEigenvalue currently has a green checkbox, 5 upvotes, an edit by a reviewer, and a favorable comment. So, at first glance, one would think my answer is wrong, since if I am right it suggests that not just one person here but the community as well is wrong also.
Nevertheless, let's see if there are any problems with NoEigenvalue's answer or if it is not as simple as it seems.
The answer starts out attempting to explain what the Fermi energy is using the Bohr model of an atom. However, it then skips to saying what Fermi energies are for some metals. It does this by referencing external tables. It entirely skips the derivation based on free electron densities, and makes no attempt to connect them. I will show that this poses a problem later, because an unstated dependence affects NoEigenvalue's argument.
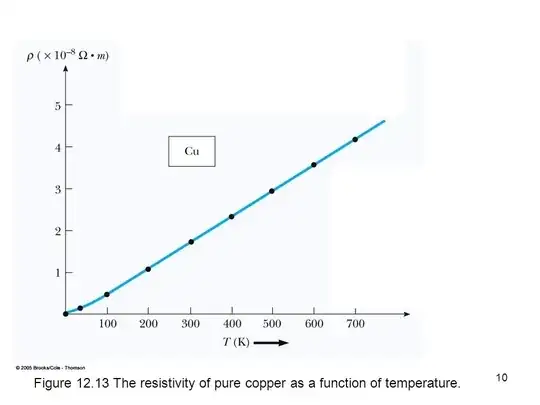
Then NoEigenvalue's answer claims, "First you must know that only electrons with an energy close to the Fermi energy can participate to the conduction process...At $T>0$...you are [only] now able to excite electrons in higher energy states, which you need to do if you want to accelerate them in a direction; i.e., if you want to do work [i.e, produce current] on them." (emphasis supplied) This argument is not explained. It is actually backwards as well. I debunked this misconception here. It is obviously false when you consider either of these metals at low temperatures, where according to the argument there would be no electrons to carry current, and conduction would be zero. In reality this is where conduction is maximized and resistivity (the inverse) approaches a minimum:
Next the author claims that $\sigma$ is defined by $ne^2\tau/m$ where $n$ is the number of electrons [per unit volume]... Wrong. The definition of conductivity is the ratio of current to field, or the ease of current flow when pushed. The cited expression largely just gives an illusion of confidence, introducing a free parameter, $\tau$, with one new equation, which doesn't necessarily give any new physical information. It thus really defines $\tau(\sigma)$, which can be argued to be a momentum exchange time scale of some electron cloud with an ionic lattice.
Next we see $\sigma=ne^2l/mv_F$ and an argument about how if $v_F$ is lower in copper than in aluminum, then the current will be higher. Not stated is that this relies upon $n$ and $l$ being the same in both metals, something that is unlikely. Indeed, this was my point made above, that a derivation of $E_F(n)$ was missing. It seems rather convenient given that it changes the later argument; aluminum is triply ionic instead of singly ionic, so $n$ gets a factor of three from that, and it ends up having a free electron density that is a factor of $21.1\times 10^{22} {\rm cm}^{-3}/8.49\times 10^{22} {\rm cm}^{-3}\simeq 2.5$ that of copper. This relatively large factor overtakes the energy/velocity one created by NoEigenvalue in an apparent attempt to make the final argument to answer a question in a simple way because that factor of a mere $11/7\simeq 1.6$ is further softened to 1.3 due to the square root function in converting from energies to velocities. So, at face value, if you include the variance of $n$ in NoEigenvalue's argument it actually would say aluminum has a greater conductivity. This clearly is a problem with the answer given that the question is why does copper have a greater conductivity.
To sum up, I think I've shown that the allegedly simple answer is both both too simple and also incorrect in many aspects. This is not a proof that the best answer is no, but it is probably a strong case that "no" is a reasonable answer if not the best answer.
At the end of the day, I think nature isn’t always so trivial as the fictional version people sometimes come up with due to their own arrogance in wanting to think they personally know what's going on and, apparently, the version of reality you seek via your question. Humility is an important partner of curiosity and good research, and one should not leave it behind in a selfish desire to trick oneself into moving forward.
 $T=0K$" />
$T=0K$" />