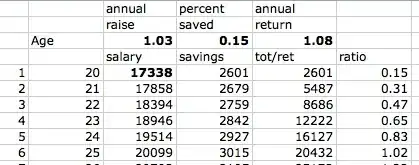
Copying a simple example from here, showing 4 deposits and 3 withdrawals.
Planning to retire in 4 months and draw monthly income of £1000 (present value) for 3 months, adjusted for inflation. APR is 8% and inflation is 4%. What should the pot be?
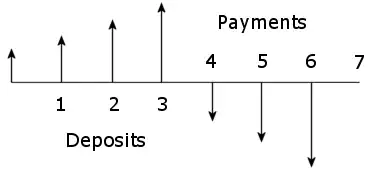
Calculating the monthly rates, assuming effective annual rates.
inf = 0.04
i = (1 + inf)^(1/12) - 1 = 0.00327374
apr = 0.08
m = (1 + apr)^(1/12) - 1 = 0.00643403
To illustrate the calculation, say we know at month 3 immediately after the final deposit, the pension pot p should be £3010.57
In month 4 it will have grown by (1 + m) and the inflation adjusted withdrawal will be w (1 + i)^4, where w = £1000. So the pension will decrease like so
p = 3010.57
p = p (1 + m) - w (1 + i)^4 = 2016.78
p = p (1 + m) - w (1 + i)^5 = 1013.28
p = p (1 + m) - w (1 + i)^6 = 0
This can be calculated in one go using a formula
o = 4 . . the month number
n = 3 . . the number of months
p = 3010.57
(-(1 + i)^(n + o) w + (1 + m)^n (i p - m p + (1 + i)^o w))/(i - m) = 0 (formula 1)
and more usefully, it can be expressed as a formula for p
p = ((1 + i)^o (1 + m)^-n ((1 + i)^n - (1 + m)^n) w)/(i - m) = 3010.57 (formula 2)
So we need £3010.57 in month 3 for inflation adjusted withdrawals of £1000.
Starting with deposit d and increasing it to compensate for inflation
p = d
p = p (1 + m) + d (1 + i)^1 = 2.00971 d
p = p (1 + m) + d (1 + i)^2 = 3.0292 d
p = p (1 + m) + d (1 + i)^3 = 4.05854 d
This can also be calculated with a formula
q = 3 . . the final month number
p = (d ((1 + i)^(1 + q) - (1 + m)^(1 + q)))/(i - m) = 4.05854 d (formula 3)
We know p = 3010.57
∴ d = 3010.57/4.05854 = 741.79
The above can be expressed as a formula for d
d = ((i - m) p)/((1 + i)^(1 + q) - (1 + m)^(1 + q)) = 741.79 (formula 4)
So the first deposit will be £741.79
The next month the deposit will be £741.79 (1 + i) = £744.21 etc.
The first withdrawal will be £1000 (1 + i)^4 = £1013.16 etc.
Putting the steps together
inf = 0.04
i = (1 + inf)^(1/12) - 1 = 0.00327374
apr = 0.08
m = (1 + apr)^(1/12) - 1 = 0.00643403
o = 4 . . the first withdrawal month number
n = 3 . . the number of withdrawal months
w = 1000 . the present value of the withdrawal amount
p = ((1 + i)^o (1 + m)^-n ((1 + i)^n - (1 + m)^n) w)/(i - m) = 3010.57
q = 3 . . the final deposit month number
d = ((i - m) p)/((1 + i)^(1 + q) - (1 + m)^(1 + q)) = 741.79
These same formulas can be used on a more realistically scaled calculation.
A more realistic calculation
For example, suppose someone at age 25 wants to withdraw $1000 per month present value from age 65 to 100. Inflation is 2% pa and interest is 3% pa (effective rates).
(65 - 25) * 12 = 480 deposit months
(100 - 65) * 12 = 420 withdrawals
(100 - 25) * 12 = 900 months overall
inf = 0.02
i = (1 + inf)^(1/12) - 1 = 0.00165158
apr = 0.03
m = (1 + apr)^(1/12) - 1 = 0.00246627
o = 480 . . the first withdrawal month number
n = 420 . . the number of withdrawal months
w = 1000 . . the present value of the withdrawal amount
p = ((1 + i)^o (1 + m)^-n ((1 + i)^n - (1 + m)^n) w)/(i - m) = 784011.41
q = 479 . . the final deposit month number
d = ((i - m) p)/((1 + i)^(1 + q) - (1 + m)^(1 + q)) = 606.00
The plan could be achieved by making 480 deposits, starting aged 25 at $606, increasing monthly in line with inflation, i.e. $607, $608, $609 etc.
The first withdrawal at age 65 will be $2208.04: $1000 present value, i.e. w (1 + i)^480.
Using formula 3 and formula 1
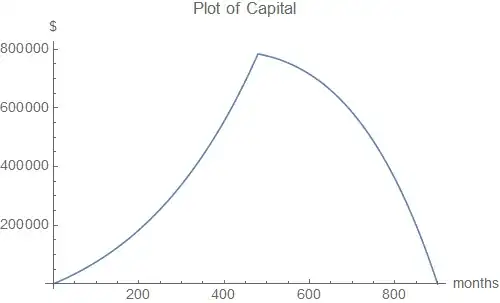
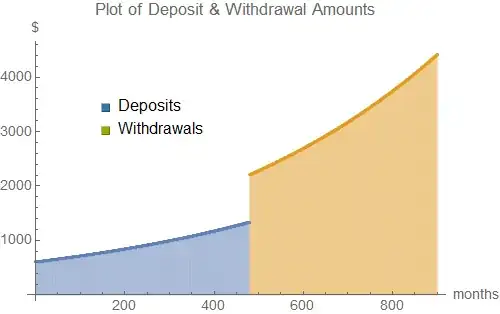
Solution for a non-depleting annuity
In fact, a non-depleting inflation-linked annuity is not possible because the withdrawals will tend to infinity, as w (1 + i)^n when n -> infinity. However, as the OP's link states ...
"The study found that retirees ... can safely withdraw 4% of their starting money each year – adjusting annually for inflation – and have more left at the end of 30 years than they started with."
the calculation for capital required can be adjusted so that it is not depleted by a certain time, in this case 420 months. So, replaying the calculation above with the formula for p adjusted.
(65 - 25) * 12 = 480 deposit months
(100 - 65) * 12 = 420 withdrawals without depleting initial capital
(100 - 25) * 12 = 900 months overall
inf = 0.02
i = (1 + inf)^(1/12) - 1 = 0.00165158
apr = 0.03
m = (1 + apr)^(1/12) - 1 = 0.00246627
o = 480 . . the first withdrawal month number
n = 420 . . the number of withdrawal months
w = 1000 . . the present value of the withdrawal amount
p = ((1 + i)^o (-(1 + i)^n + (1 + m)^n) w)/((-i + m) (-1 - m + (1 + m)^n))
= 1217900.47 (formula 5)
q = 479 . . the final deposit month number
d = ((i - m) p)/((1 + i)^(1 + q) - (1 + m)^(1 + q)) = 941.38
The plan could be achieved by making 480 deposits, starting aged 25 at $941.38, increasing monthly in line with inflation.
Again, the first withdrawal at age 65 will be $2208.04: $1000 present value, i.e. w (1 + i)^480.
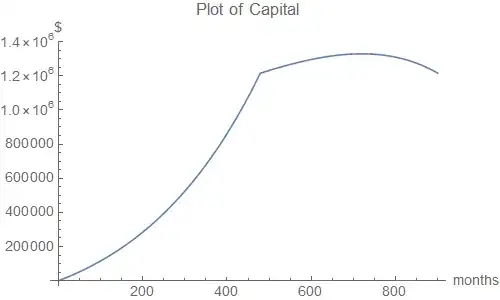
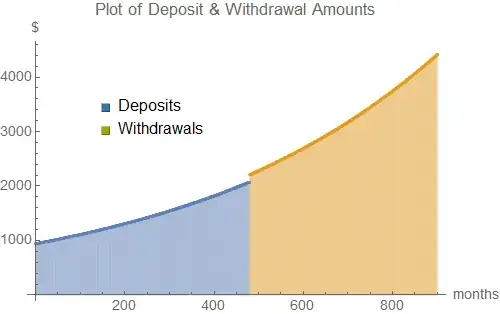
The plot of capital can be extended by taking values of n beyond 420 months, illustrating how the inflation-linked withdrawals outpace the capital growth.
When will I reach a state, where my investment's monthly returns will be equal to my monthly expenses?
This is the OP's question, clarified in the comments. Without considering inflation the answer is straightforward. With effective APR of 3% and monthly deposit/withdrawals of $1000.
apr = 0.03
m = (1 + apr)^(1/12) - 1 = 0.00246627
d = w = 1000
p = w/m = 405470.65 . . capital required
n = Log[1 + (m p)/(d + d m)]/Log[1 + m] = 280.898 (formula 6)
So in 23 years and 5 months (281 months) the capital will not diminish.
With inflation
The same calculation compensating for inflation is more involved. With inflation at 2% and APR at 3%, deposits and withdrawals at $1000 present value.
inf = 0.02
i = (1 + inf)^(1/12) - 1 = 0.00165158
apr = 0.03
m = (1 + apr)^(1/12) - 1 = 0.00246627
Try 35 years of deposits
years = 35
d = 1000
q = years*12 - 1
o = q + 1
w = 1000
p = (d ((1 + i)^(1 + q) - (1 + m)^(1 + q)))/(i - m) = 999121.67
Using formula 5
solve ((1 + i)^o (-(1 + i)^n + (1 + m)^n) w)/((-i + m) (-1 - m + (1 + m)^n)) = p for n
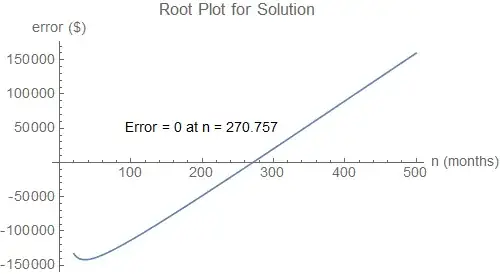
n = 270.757
So with 35 years of deposits the capital will not diminish for 22 years and 6 months (270 months).
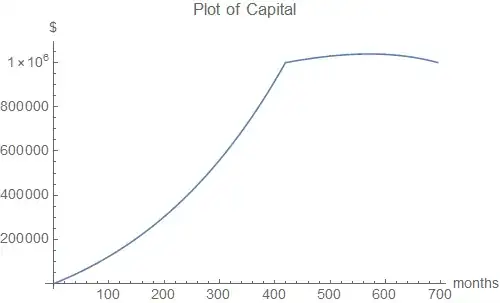
Rerunning the calculation for a range of deposit spans shows that for a 30 year period of withdrawals without diminished capital, 36 years and 10 months of savings would be required.
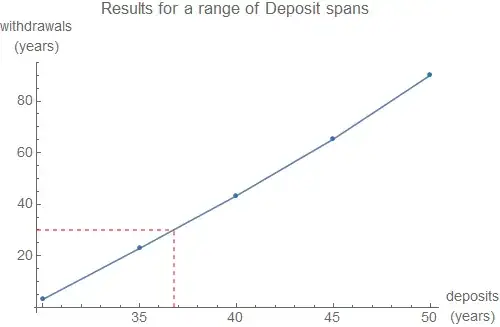
As previously mentioned, these inflation-linked calculations base all the deposits and withdrawals on present value, at the time of the first deposit. So in the examples above, if the deposits start today, all the future withdrawals will be worth $1000 in today's money.
Formulae derivations
The main formulae are derived from fairly simple recurrence equations, solved using Mathematica.
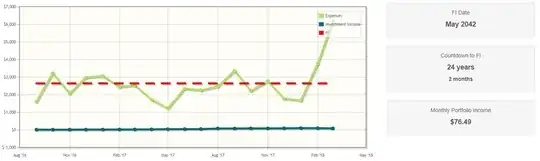But to motivate me a bit more, I wanted to calculate the FI date on my own after each month so I would be able to create a graph of how far away I am. To see if I progress after each month or not.
