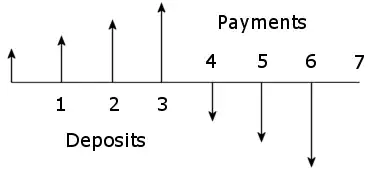
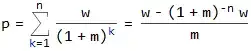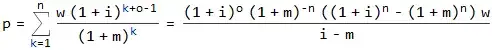As a follow-up to this question, what is the minimum size of a nest egg to support 30 years of $5,583.33 monthly distributions? I want the $5,583.33 to increase with inflation each month.
The present value of the first payment should be $5,583.33.
First withdrawal will be in 20 years: $5,583.33*(1 + 0.0033)^240 = $12,310.86
Here is what I've pieced together from this question:
Total withdrawals: n = (30 years)(12 months) = 360 payments
Inflation per period: i = 4.0% per year / 12 = 0.3333% per period)
Return per period: m = 8.0% per year / 12 = 0.6666% per period)
Periods until 1st payment: o = (20 years)(12 months) = 240 periods
First payment amount: w = $67,000 / 12 = $5,583.33 (today's dollars)
p = ([(1 + i)^o]*[(1 + m)^-n]*((1 + i)^n - (1 + m)^n)*w)/(i - m)
p = ([(1 + 0.0033)^240]*[(1 + 0.00667)^-360]*((1 + 0.0033)^360 - (1 + 0.00667)^360)*5583.33)/(0.00333 - 0.00667)
p = $2,594,790.06
where
n is the number of payments to be received
o is the number of the period at the end of which the first payment is received
w is the payment amount
m is the pension fund's periodic rate of return
i is the periodic inflation rate
Is this the right equation? From what I could find on Google, this calculation is called the present value of a growing or graduated annuity. Is this correct?
Is it correct to say that $2.5 million is the nest egg balance 20 years from now on the day the first withdrawal is made? And that $2.5 million is not in today's dollars but in equivalent dollars 20 years from now?