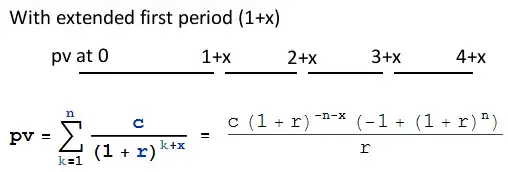Calculating interest accrued with extended Initial Payment Date

Question

I'm wondering how do I calculate the interest accrued if the intervals aren't perfect. For example

Principal - $100,000
Interest - 8%
Compounding monthly
Disbursal Date - January 1st, 2016
Initial Payment Date - February 11, 2016

I can calculate it if it's exactly 1 month then the time passed would be 1/12.

Interest accrued = ((1 + i / cf)^(cf)*T - 1) * principal balance

Where cf is compound frequency, T is time.

If duration that has passed is exactly 1 month, the interest accrued is 666.67. The interest accrued to the original question is $887.31, but I'm unsure how to get that value.

Answer's here https://i.snag.gy/lMYorT.jpg

Answer 1

You need to do detective work to see how the lender is treating loan periods of less than a month. Fortunately, there's enough information to do the job, without knowing the assumptions. The thing to remember is that the interest rate and how to apply it is a fluid number, subject to exaggeration, inflation, and deceit, but the payment schedule is real and concrete. So...

First, calculate the principal amount of an ordinary annuity, at 0.6666666% per month, that is paid off by 36 monthly payments of $3140.50 Use a mortgage calculator, or this formula:

This turns out to be $100,219.03. This is the present value of an ordinary annuity which starts, naturally enough, one month before the first payment, or on Jan 11

Now, that is the present value of the mortgage of Jan 11. We can now switch to monthly compounding. Multiplying this Jan 11 value by a months interest, 1.0066666666666, gives a value as of the first payment on February 11, of $100,887.15 So the original debt has grown by the addition of $887.15 of interest.

As to justifying this amount of interest for the first part of the loan, that would require a knowledge of how the lender chose to treat partial periods. Trying this guess:

1. Take the 8% per year, compounded monthly
2. Divide by 12 and add 1 to get the monthly growth factor; 1.0066666666
3. Raise this monthly growth factor to the 12th power to get the effective annual growth factor;
4. Raise this annual growth factor to the (1/365) power to get the daily growth factor
5. Raise this daily growth factor to the 10th power to get the growth factor for 10 days;
6. Multiply by the original $100,000

And we get..... 100218.68, not the 100,219.03

So the method above is not the one the lender has chosen to apply. (Unless rounding errors are included...)

Answer 2

The formula for a loan is worked out by equating the present value of the loan to the sum of the payments discounted to present value by the interest rate and period. (The summation is converted to a formula by induction.)

So for a standard loan with equal payment periods we have the formula below. (This is the same as the formula quoted by DJohnM.)

With an extended first period the formula is modified like so.

We can work out the extension x

Treat Jan 1st to Feb 11th as an average month plus 10 days. (Jan 1st to Feb 1st is an average month; Feb 1st to Feb 11th is 10 days.)

x is 10 fractions of an average month.

x = 10/(365/12)

pv = 100000
n = 36
r = 0.08/12

Using the formula for an extended first period

pv = (c (1 + r)^(-n - x) (-1 + (1 + r)^n))/r

∴ c = (pv r (1 + r)^(n + x))/(-1 + (1 + r)^n)

∴ c = 3140.489480141824

The regular repayment is $3,140.49

Answer 3

I reached out to TValues and here's the solution they've provided.

Interest for 1 month is 666.67

So now you have to find the interest accrued from Feb1st to Feb 11 (10 days0

So it now becomes 100666.67 * (.08/365)*10 = 220.64 is the amount of interest accrued from feb 1 to feb 11.

Add the two interest accrued, you get 887.30