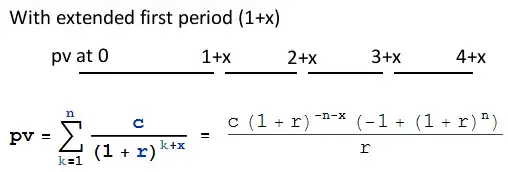Calculate a weekly payment on a loan when payment is a month away

Question

I'm trying to calculate a payment on a loan given the standard P=r(PV)/1-(1+r)^-n formula. How do I factor in interest accumulated if the first payment isn't due for 31 days? For reference, interest rate = 21, No pmts = 52, Amt financed = 8764.65. I'm anticipating a payment of 189.78 (based on a third party program's calculation)

Answer 1

At time = 0, no interest has accrued. That's normal. And the first payment is due after a month, when there's a month's interest and a bit of principal due.

Note - I missed weekly payments. You'd have to account for this manually, add a month's interest, then calculate based on weekly payments.

Answer 2

Using the standard loan formula with 21% APR nominal, compounded weekly.

Calculate an adjusted loan start value by adding 31 - 7 = 24 extra days of daily interest (by converting the nominal compounded weekly rate to a daily rate).

For details see Converting between compounding frequencies

 dailyrate = ((1 + 0.21/52)^(52/365)) - 1

 pv = 8764.65*(1 + dailyrate)^24 = 8886.27

 n = 52
 r = 0.21/52

Applying the standard formula r (pv)/(1 - (1 + r)^-n) = 189.80

So every weekly payment will be 189.80

Alternatively

Directly arriving at the same result by using the loan formula described here,

The extension x is 31 - 7 = 24 daily fractions of an average week (where 7 daily fractions of an average week equal one average week).

x = (31 - 7)/(365/52)

pv = 8764.65
n = 52
r = 0.21/52

pv = (c (1 + r)^(-n - x) (-1 + (1 + r)^n))/r

∴ c = (pv r (1 + r)^(n + x))/(-1 + (1 + r)^n)

∴ c = 189.80

As before, the weekly payment will be 189.80

Both methods are effectively the same calculation.

Answer 3

You'd have to look at the terms of the loan to be sure, but if the interest compounds weekly then you'd have to calculate the effect of 3 compounding periods, then compute for weekly payments. The balance after 3 weeks would be:

8764.65 * (1 + .21/52) ^ 3 = 8871.27

Using Excel's PMT function for that principal balance, I get a weekly payment of $189.48.

If the interest doesn't compound, the principal balance will be about $8888.37 and the weekly payment would be $189.85.

Note, however, that the terms of the loan could be completely customized, so you'd need to be sure that the payment and the amortization schedule make sense to you before you agree to the loan. Since the interest is very high, I suspect this is a "no credit needed" car loan which are notorious for unfavorable (to the borrower) terms.