How does this retirement fund calculator work?

Question

I found a retirement fund calculator on web:

                 Inflation rate:       2%          0%          2%          0% 
           Expected return rate:       5%          0%          0%          5%
                    Current age:       30          30          30          30
                 Retirement Age:       65          65          65          65
         Years after retirement:       15          15          15          15
            Monthly expenditure:   $10000      $10000      $10000      $10000
                                ----------  ----------  ----------  ----------            
Required fund at retirement age: $2961797    $1800000    $4150191    $1307837

I'd like to know how I can reproduce the calculation formulas in Excel?

Answer 1

I wasn't able to get a formula that matched those numbers precisely, but I think I got close enough to what you are looking for.

If your first column of numbers was B1:B6 the formula in B7 would look like this:

=PV((1+B2/1+B1-1)/12,15*12,-FV(B1,B4-B3,,-B6),,1)

The first argument to the PV function is the inflation adjusted rate of return, the second is the number of monthly expeditures, the third is the inflation adjusted monthly expenditure, and the fifth signifies money required upfront.

The fv function calculates inflation adjusted monthly expenditure from the inflation rate, years until retirement, and the current value of the monthly expenditure.

I don't know what I missed but my numbers are close, so you can get a good idea from this formula.

Answer 2

I have put together a method for assessing the size of the pot. It uses the european method of compounding though.

I realise it doesn't use Excel, (actually I'm using Mathematica), but the calculations are fairly legible and it should be quite straightforward to implement the method using other tools.

The calculation assumes the pension payouts are in present value terms, so if you wanted £10,000 in 35 years, accounting for inflation at 2% that would be £19,998.90.

I've gone through the steps first with small numbers:-

Planning to retire in 4 months and draw monthly income of £1000 (present value) for 3 months, adjusted for inflation. APR is 8% and inflation is 4%. What should the pot be?

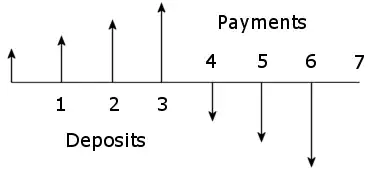
Therefore need a pot at month 4 that can deliver these payment at months 4, 5 & 6 with APR = 8%

So for the root calculation t[0] is 1, t[1] is 0.5 and t[2] is 0.

Ref: http://en.wikipedia.org/wiki/Rate_of_return#Internal_rate_of_return

Checking: amounts remaining in the pot after month n, using monthly rate m

Pot is empty after month 6, so everything seems to work.

Edit

After reviewing this calculation, it can be done more simply:-

inf = 0.04;
i = (1 + inf)^(1/12) - 1

0.00327374

apr = 0.08;
m = (1 + apr)^(1/12) - 1

0.00643403

calc = Function[n, 1000 (1 + i)^n (1 + m)^-(n - 4)];
discountedpayouts = Map[calc, {4, 5, 6}]

{1013.16, 1009.98, 1006.81}

pensionpot = Total[discountedpayouts]

3029.94

The same method can be used for the calculation over 50 years.

End of edit

Now running a generalised version with £10,000 (present value) payouts with inflation at 2% and APR 5%, as specified by the OP.

This finds a pot requirement of £2,922,808 which is a little different to the OP's result, most likely due to the difference between the US and EU formulations of APR and compounding methods.

Switching inflation and APR to 0% yields £1,800,000.

Inflation at 2% and APR at 0% yields £4,188,098.

Inflation at 0% and APR at 5% yields £1,279,041.

I'll try to post an inflation based calculation for the deposits later.