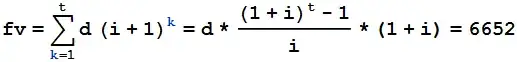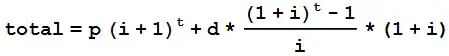I am familiar with the formula for calculating FV and compound interest of a deposit, but I am wondering if there is a formula that will allow me to calculate how much money I will have after depositing recurring amount of money every month, quarter or year, with a fixed annual interest rate and an optional initial deposit?
Let's say:
Initial/present value: 2500
Annual interest: 4%
Recurring deposit every month: 100
How much will the FV be after 5 years?
Using the following values:
p = initial value = 2500
n = compounding periods per year = 12
r = nominal interest rate, compounded n times per year = 4% = 0.04
i = periodic interest rate = r/n = 0.04/12 = 0.00333333
y = number of years = 5
t = number of compounding periods = n*y = 12*5 = 60
d = periodic deposit = 100
The formula for the future value of an annuity due is d*(((1 + i)^t - 1)/i)*(1 + i)
(In an annuity due, a deposit is made at the beginning of a period and the interest is received at the end of the period. This is in contrast to an ordinary annuity, where a payment is made at the end of a period.)
See Calculating The Present And Future Value Of Annuities
The formula is derived, by induction, from the summation of the future values of every deposit.
The initial value, with interest accumulated for all periods, can simply be added.
pfv = p*(1 + i)^t = 3052.49
total = pfv + fv = 3052.49 + 6652 = 9704.49
So the overall formula is
Let's break this into two parts, the future value of the initial deposit, and the future value of the payments:
D(1 + i)n
For the future value of the payments
A((1+i)n-1) / i)
Adding those two formulas together will give you the amount of money that should be in your account at the end. Remember to make the appropriate adjustments to interest rate and the number of payments. Divide the interest rate by the number of periods in a year (four for quarterly, twelve for monthly), and multiply the number of periods (p) by the same number. Of course the monthly deposit amount will need to be in the same terms.
See also: Annuity (finance theory) - Wikipedia
I noticed there did not necessarily seem to be a caveat for adjusting contribution frequency. I have included a formula below that would take this into account.
A = P(1+r/n)^(nt) + c[a(1 - r/n)^(nfz)] / [1 - (1 + r/n)^(nf)]
P = Principal r = interest rate n = number of compounds per year t = number of years this is compounding c = the amount of the contributions made each period a = will be one of two things depending on when contributions are made [if made at the end of the period, a = 1. If made at the beginning of the period, a = (1 + r/n)^(n*f)] f = frequency of contributions in years (so if monthly, f = 1/12) z = the number of contributions you would make over the life of the account (typically this would be t/f)
For example, suppose I had $10,000 in an account compounding daily at 4%. If I make contributions monthly of $100, then what is the value in 10 years? This would be set up accordingly.
Contributions made at the end of the month: A = 10,000(1 + 0.04/365)^(365 * 10) + 100[1(1 - 0.04/365)^(365 1/12(10/(1/12))] / [1 - (1 + 0.04/365)^(365*1/12)]
Simplifying: A = 10,000(1 + 0.04/365)^(3,650) + 100[1(1 - 0.04/365)^(3,650)] / [1 - (1 + 0.04/365)^(365/12)] A = $29,647.91
Contributions made at the beginning of the month: A = 10,000(1 + 0.04/365)^(365 * 10) + 100[(1 + 0.04/365)^(365*1/12)(1 - 0.04/365)^(365 1/12(10/(1/12))] / [1 - (1 + 0.04/365)^(365*1/12)]
Simplifying: A = 10,000(1 + 0.04/365)^(3,650) + 100[(1 + 0.04/365)^(365/12)(1 - 0.04/365)^(3,650)] / [1 - (1 + 0.04/365)^(365/12)] A = $29,697.09
