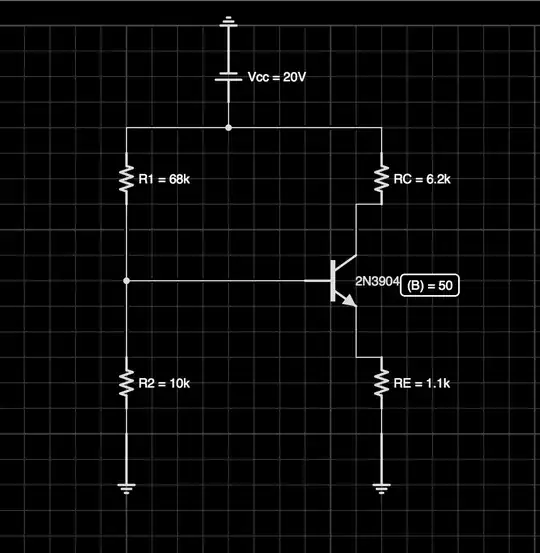
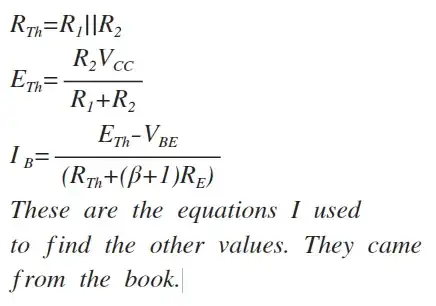The question gives the following schematic and says to find the Q point for the Voltage(Collector to Emitter) and the Q point for the Collector Current. It gives beta as 50.
I'm using two standard equations from my book to find the (Q) point for the Voltage(Collector to Emitter) and the Collector Current. I followed step by step instructions from the book and I'm being told I'm wrong. Could someone calculate these two values and maybe tell me where I went wrong.
I'm told that when finding the (Q) point I can't use these two equations because (B) beta is completely independent. But when I look in my book all the equations are identical to the ones finding a value related to a (Q) point. I've listed the equations below with my answers.