Were vacuum tube computers made of logic gates?

Question

A lot of introductory resources on modern CPU present them as being built from NAND gates (see here and there for instance).

Actually, it is possible to build a modern CPU using almost exclusively that single component, because of functional completeness (see NAND logic) and because a NAND gate is something not too difficult to conceive from CMOS transistors (see here).

Now, if we wanted to explain how vacuum tube computer were conceived, before the advent of semi-conductors, would a description based on logic gates be accurate?

Answer 1

There were a lot of variations of vacuum tube computers. The idea of carrying out computations electronically was new, and the folks hadn't quite nailed down the mathematics of it, never mind having figured out the most efficient way to store and operate on numbers electronically.

ENIAC was one of the first (if not the very first) electronic computer. Whether you want to call it the first depends on where you draw the line between calculator and computer.

From today's perspective, ENIAC was bizarre. It didn't work in binary. It operated natively on decimal numbers. Where today we have bits representing 1 and 0 and then group them in bytes or other larger groups for larger numbers, ENIAC used a ten position ring counter with carry output to represent a standard decimal digit as its smallest storage unit.

This was a carry over from mechanical calculators, so it was easier for the folks who were used to the older equipment to conceive and construct.

It took 36 tubes in the ENIAC to represent one digit. A modern binary system can store 4 bits (allowing values from 0 to 15 to be stored) in four flip-flops, each with two transistors for 8 transistors total. You can build an equivalent flip-flop with tubes. A four bit storage unit with tubes would have only take 8 tubes.

It seems obvious today that you want to use binary to represent your numbers, but it wasn't obvious back then. With a ring counter for digit storage, you get adding and carry as part of the function - you have to add more logic for adding and such to the binary memory. Without an overview of the situation, it is hard to tell which will end up being simpler and more efficient.

With time, it became clear that it was simpler and more efficient for the machines to work in binary, even though that meant your programmers and system engineers had to learn to work in a different numerical base.

You could build a vacuum tube computer entirely out of NAND gates. A vacuum tube functions similar to a transistor, so you could duplicate any transistor logic circuit with tubes.

You probably wouldn't want to do that, though. If you use only NAND gates, you will sometimes have to use multiple gates to build a specific logic funtion. An AND gate is a NAND gate followed by a NAND gate wired to make a NOT gate. That takes more transistors (and tubes) than building an AND gate. Individual tubes cost far more than individual transistors and they fail very often - you want to reduce the number of tubes to reduce costs and failures. You'd build each logic circuit of the appropriate type rather than assembling them from NAND gates.

Answer 2

Here is one of the early papers. The early computer designers didn't think in "logic gate" terms. The basic flip flop was cross-coupled inverters clocked from the cathodes. There was much capacitive coupling: computation often utilized trains of pulses instead of static levels.

Edit:

And here's another example. From a logic viewpoint, the tube is a two-output gate, ~(A&B) along with A&~B. But you won't see that in the patent. This is different from a CMOS implementation: logic using differential amplifiers in this way is very rare (extinct?) these days.

Yet another edit:

If you're building a computer from NAND gates, your basic bistable element is going to be something like this:

^{simulate this circuit – Schematic created using CircuitLab}

But you never see anything like this in early papers or books. This seems not to have been part of the conceptual framework the early designers used. The internal switching within early flip-flops doesn't even match the architecture of early gates, even though that was a possibility. The early papers and books put bistable circuits before logic, which indicates that the authors considered logic to have a supporting role, not a central one. The idea of something like NAND as a universal building block was not present.

Still another edit:

electronics.stackexchange.com/questions/318341/… suggests that the modern edge-triggered flip flop, composed of Boolean gates, appeared in the 1960s. Before that, edge triggering was widespread, but implemented with capacitors, a distinctly non Boolean approach.

Answer 3

Vacuum tube computers were made of logic gates

Logic Gate theory dates back to Leibniz's 1690 discovery of his algebra of concepts (deductively equivalent to the Boolean algebra). Also see A Survey of Symbolic Logic by Lewis, UC Press Berkley 1918.

The use of digital logic elements such as AND, XOR, etc., were well understood before the first digital computers. Boolean algebra was introduced in the period of 1847 to 1854 and formally introduced as Boolean Algebra in 1913. To quote Wikipedia "Boolean algebra has been fundamental in the development of digital electronics, ...".

For example, the patent for an AND gate by Tesla US Patent No. 725,605 on 14 April 1903. Walther Bothe, inventor of the coincidence circuit, got part of the 1954 Nobel Prize in physics, for the first modern electronic AND gate in 1924.

Prior to vacuum tube computers there were earlier mechanical calculating devices refer to papers such as relay switching circuits

Just because a computer was designed for calculating decimal numbers didn't mean that they did not include binary logic gate circuits.

Konrad Zuse designed and built electromechanical logic gates for his computer Z1 (from 1935 to 1938). His binary computer predates the US computers, to quote from Wikipedia:

His greatest achievement was the world's first programmable computer; the functional program-controlled Turing-complete Z3 became operational in May 1941. Thanks to this machine and its predecessors, Zuse is regarded by some as the inventor and father of the modern computer.

Zuse was noted for the S2 computing machine, considered the first process control computer. In 1941, he founded one of the earliest computer businesses, producing the Z4, which became the world's first commercial computer. From 1943 to 1945 he designed Plankalkül, the first high-level programming language. In 1969, Zuse suggested the concept of a computation-based universe in his book

Rechnender Raum (Calculating Space).

Much of his early work was financed by his family and commerce, but after 1939 he was given resources by the government of Nazi Germany. Due to World War II, Zuse's work went largely unnoticed in the United Kingdom and United States. Possibly his first documented influence on a US company was IBM's option on his patents in 1946.

In 1938 there was Claude Shannon's paper on switching circuits and Boolean Algebra.

Text books of the vacuum tube era described the design of digital computer circuits using logic gates.

Jacob Millman helped develop RADAR systems and wrote 8 books on electronics. These books included the Millman and Taub, Pulse and Digital Circuits, McGraw Hill 1956, Library of Congress 55-11930 VIII 42385. Chapter 5, The Bistable Multivibrator, Pages 140-173. In these 34 pages they describe the theory and application of vacuum tube pulse techniques for systems like RADAR, frequency counters, etc. Absent was any mention of digital computer design.

Like the previous 4 introductory electronics chapters from 'Review of Amplifier Circuits' to 'Non-Linear Wave Shaping' and the following 7 chapters which continued analysis in terms of pulse techniques for circuits ranging from 'Monostable and Astable Multivibrators' to 'Synchronization and Frequency Division'.

Chapter 13, 'Digital Computer Circuits', Pages 392-428 details the circuit operation of OR, AND, NOT and XOR in terms of Boolean Algebra. When describing a register that was built using the available technology it would now be described as an RS Flip-Flop the chapter has these illustration:

This book along with the other 1940s and 50s references predates the 1962 MIL-STD-806B which defines our current drawing symbol set. Historically logic gates were just drawn as square boxes, e.g. Millman and Taub, Fig 13-28 Page 414, Fig 13-35 Page 421, Table 13-1 Page 420 above, or the below referenced IBM 704 Logic Symbols, 704_schemVol1.pdf, Page 4:

It was impossible for these earlier references to draw their computer designs using a symbol drawing set that didn't exist.

To quote from Wikipedia's Karnaugh map entry:

The Karnaugh map (KM or K-map) is a method of simplifying Boolean algebra expressions. Maurice Karnaugh introduced it in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which was a rediscovery of Allan Marquand's 1881 logical diagram aka Marquand diagram but with a focus now set on its utility for switching circuits. Veitch charts are also known as Marquand–Veitch diagrams or, rarely, as Svoboda charts, and Karnaugh maps as Karnaugh–Veitch maps (KV maps).

Therefore digital logic elements were well understood when the first vacuum tube computers were designed.

Logic elements such as AND, OR and Inverters were used in the design of early vacuum tube computers. Wikipedia entry for IBM states:

It offered its first commercial stored-program computer, the vacuum tube based IBM 701, in 1952.

Bitsavers in the Computing Archive contains reference material for early computers from various manufacturers. In the IBM 701 folder there is an extract from the Proceedings of the Institute of Radio Engineers (I.R.E). For all publications see Proceedings 1913 to 1962. In 1963 the name was changed to Institute of Electrical and Electronics Engineers (IEEE).

The October 1953 extract (Buchholz_IBM_701_System_Design_Oct53.pdf), Page 1262, System Design of the IBM Type 701 Computer. This provides an introduction to the system. Starting on Page 1287 is the article The Arithmetic Element of the IBM Type 701 Computer. Page 1289 has the Circuit Operation section which includes a diagram of an adder constructed of AND, OR and NOT gates.

The bitsavers site also has the engineering diagrams for the IBM 704 (e.g. 704_schemVol1.pdf) IBM 704 computer which was introduced in 1954. As an example, the System Diagrams in the Volume 1 schematics book uses AND, OR logic gates.

At one time I had engineering drawings for the UNIVAC I and that used blocks of logic. Unfortunately these drawings are long gone and I cannot provide references to that material.

In reference to the question posed, a description based on logic gates is appropriate.

To implement these logic elements refer to material such as:

• More Reliable Vacuum Tubes Designed for Digital Circuits are Produced To extend the life of vacuum tubes they could be run with a lower heater voltage but this introduced problems with cathode poisioning. Therefore variants were produced for digital logic circuits such as those used in computers. Also see Colossus, the first large-scale electronic computer.
• Let’s Build Some Logic Gates out of Vacuum Tubes: OR, NOR, NAND, AND
• Vacuum Tube Computer P.01 – Architecture and the MC14500B
• Basic Principles of Vacuum Tube Logic Circuits

Answer 4

Electronic computers need to have controllable switches to construct Boolean logic functions, including gates. Vacuum tube-based digital computers were no different. So, yes, vacuum tube machines being digital computers composed of binary logic, used ‘gates’ by definition.

The basic concepts of binary logic were well-known in the 1940s. Boolean math (symbolic logic) as a formal discipline had been studied, taught and used for at least a hundred years by that time, based on ideas going as far back as Aristotle. A symbology for Boolean math had been in place for at least forty years. Two-value Boolean algebra was the subject of several influential scholarly papers in the mid-1930s.

The takeaway is, the formal and practical underpinnings of 2-state Boolean logic were already established by the time tube computers came along.

It’s not clear (to me, anyway) when the term ‘logic gate’ came into use. In the 1930s the electronic ‘coincidence circuit’ (AND) function was first described and built. Even before then, electomechanical relays were used to implement logic and build computers, a practice that persisted into the tube era.

The point being, binary gates as a concept existed well before vacuum tube computers. A binary logic function by any other name, be it a ‘gate’ or a ‘coincidence detector’ is still a logic function.

Back to tubes. How are they used to make binary logic? Tubes are voltage-controlled current switches that work something like FETs (specifically, JFETs.) Their ability to switch can be used to create logic gates.

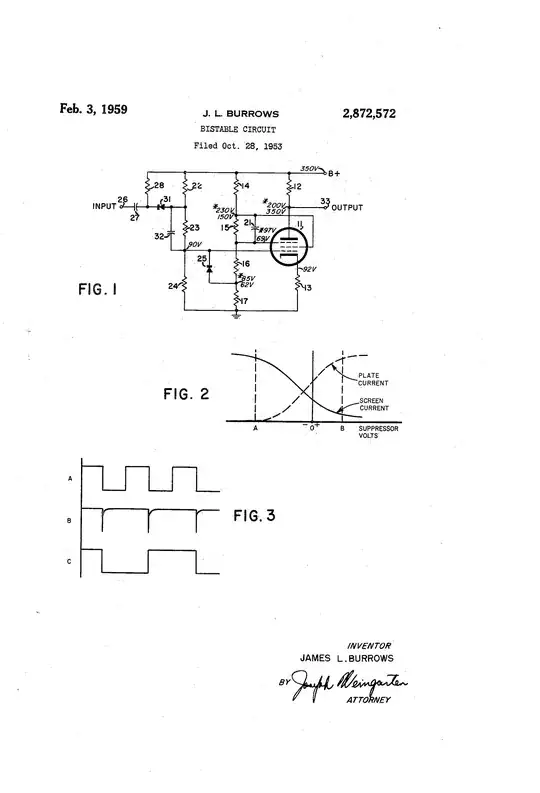
How exactly did the early designers do that? For starters, tubes have some rather unfriendly biasing requirements, requiring different thinking than you’re used to regarding logic levels. High operating voltages and complex level shifting were the norm.

More here: NOT gate using triodes

Second, the very earliest machines didn’t necessarily use power-of-2 word-size binary like we do today. Some, like ENIAC, worked in base-10, and used electronic analogues of mechanical systems. Later machines like the IBM 7xx adopted more conventional binary base-16 working.

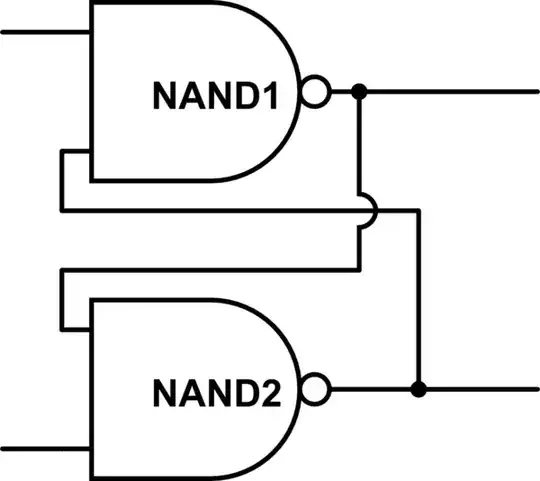
You mentioned the NAND as a ‘universal gate’. Did vacuum tube machines use a ‘universal gate’? The answer is, nope.

Using all-NAND is more of a CMOS thing; tubes not so much. For that matter, even CMOS machines don’t use all-NAND, but will use a variety of structures to yield the best trade off of speed, area, and power. And so it goes with tubes.

Let’s touch on this 'universal gate' idea for a bit.

First, NOR gates can be used with equal efficiency as NAND as the ‘universal gate’. And in fact, to my knowledge, only one practical machine has been constructed from just one gate type, be it NAND or NOR: the Apollo Guidance Computer. The AGC's CPU was built using just one type of logic IC, a dual 3-input NOR.

More here: What is the lowest level of CPU programming above transistors?

tl; dr: The AGC’s designers did that because they could manage the spaceflight-level reliability issues by settling on just one logic IC. It was a radical and somewhat controversial idea at the time, but it worked well.

Meanwhile, back on Earth, we don’t have to get hung up on a single gate type being a fundamental logic unit. You have a bit more flexibility.

When it comes to tubes, you have to think at a lower level than gates. After all, tubes are bulky, expensive, power-hungry, and have limited life. Using them efficiently requires some creative thinking.

And indeed, those tube-machine designers did exactly that. They standardized on a select few tube types, from which they fashioned the basic elements they needed - AND, OR, NOT, NAND, NOR, XOR, flip-flop etc. They worked out the biasing and connection schemes to make them work together, meanwhile working very hard to minimize the tube count.

That said, the closest thing to a ‘universal’ tube logic element would be the dual triode tube. This tube, through various connection schemes, could render a gate, flip-flop, or switch.

Diode tubes also saw some use. Tetrodes and pentodes proved handy for making AND gates owing to their multiple grids.

There were some exotic tube types, including counting tubes that modeled mechanical systems, such as the cold-cathode Dekatrons used in ANITA calculators.

Later machines, including the IBM 604 keypunch linked above and 704 used semiconductor diodes to replace diode tubes.

Answer 5

Now, if we wanted to explain how vacuum tube computer were conceived, before the advent of semi-conductors, would a description based on logic gates be accurate?

Logic gates have nothing to do with semiconductors. They are abstract mathematical primitives that happen to be a graphical representation of propositional logic formulas. A combinatorial logic circuit diagram is, ignoring timing, exactly equivalent to a propositional logic formula.

Asking whether a description "based on logic gates" would be accurate for combinatorial functions in a digital computer is like asking whether propositional logic can describe them. Of course it does, they were all designed with propositional logic in one form or another first, and only later converter to physical circuits.

Now, how straightforward is the translation of propositional logic formulas (a.k.a. logic gate circuit diagrams) to electronic building blocks such as vacuum tubes, bipolar transistors, or mos transistors, and the accompanying passive components - that's a whole another story, and the translation can be quite complex!

Once timing is added into the description, the logic gates don't represent propositional formulas, but rather temporal state propagation graphs overlaid on top of propositional logic primitives. They are still abstract mathematical representations, but most engineers don't reason about them that way. Analysis tools, on the other hands, have to.