RC snubber causing latch in relay

Question

I'm driving an RT314730 relay directly with an MOC3063:

^{simulate this circuit – Schematic created using CircuitLab}

The problem is when SW1 is open the relay latches. I tried 10nF instead of 100nF and the relay oscillates. If I remove the RC snubber, the circuit works as intended.

I have to mention that the opto-coupler is not from ONsemi:

Why does the relay latch with a snubber in place?

---

Update: There was an inrush current (I guess?) when I plugged in the circuit and for whatever reason it caused the relay to latch, by adding a 47nF/400V capacitor parallel to the AC line the problem is solved.

Answer 1

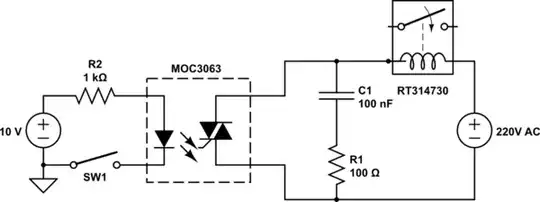
Some ideas for you to consider:
1. Use the correct opto-isolator.
The MOC3063 is not intended to drive a load directly, it is designed to trigger a TRIAC, which is not the same function as driving a relay coil, refer last page of the datasheet, screenshot below:

2. Snubber design.
To design a snubber in a switching application (such as this), you need to have the following data:

1. A good electrical model of the load that is being switched.

2. A good understanding of what the snubber is intended to do, for example:
   (a) Protect the load from harsh di/dt and/or dv/dt, and from over-voltage & over-current.
   (b) Protect the switching device from harsh di/dt and/or dv/dt, and from over-voltage & over-current.
   (c) Mitigate EMI (electromagnetic interference).
   (d) A combination of the above.

3. A set of requirements of what the voltage and current waveforms should look like (for both the load, and the switching device) during (a) turn-on and (b) turn-off.

I can help with item (1). However, for items (2) & (3) I would need extra data about your application, and it is greatly dependent on the switching device being used (which we know from point 1 of my answer that the MMOC3063 is not the best choice here). Also, it can become a complex process if you want to do it properly, so let's ignore this for now.

Update 2023-12-04:
After the data is available, and it comes time to design an RC snubber to suit an inductive load, this will be a useful starting point:-
How to design an RC snubber for a solenoid relay driving an inductive load??

2.1. Determining a model for the load.
In this case, the relay coil is the load, and you need to work out its equivalent circuit. Let's assume it can modeled as a series connection of an R and an L. The value for R is provided by the datasheet, but the value for L is not provided directly, but it can be computed by using the coil data, refer screenshot below:

Assuming you are using the coil rated for 230VAC, we see that "Coil resistance" is 32.5kΩ, and "Rated coil power VA" is 0.74VA. Now, just to check we are on the right path here, we can ask the question: "If the coil had no inductance, what would be the VA rating we would expect?" Let's calculate the VA rating at the rated voltage (230VAC 50/60Hz) due purely to the resistance, which we can calculate from the current that would flow in the coil:
Icoil = 230VAC / 32.5kΩ = 7.08mA.
VAcoil = 230VAC x 7.08mA = 1.63VA (in this case, the VA can be replaced with watts, since the load is purely resistive).

We see that 1.63VA is much larger than the stated VA rating of 0.74VA. That means that this coil has significant inductance, which would impact any snubber design.

Some simple complex number arithmetic allows us to compute the impedance of L, from which we can then compute L, assuming AC frequency (50Hz):

Icoil = 0.74VA / 230V = 3.22mA.
|Zcoil| = 230V / 3.22mA = 71.5kΩ.
Where "|..|" notation indicates the magnitude of a complex number. Now, let's use "XL" as the impedance of the coil inductance, and "^2" to mean "squared", we can write:
|Zcoil|^2 = R^2 + |XL|^2 (from Pythagoras.)
|XL|^2 = |Zcoil|^2 - R^2.

Plugging in the values, we find that:
|XL|^2 = (71.5kΩ)^2 - (32.5kΩ)^2
= 4.056E+09
|XL| = 63.7kΩ. Which is much larger than the coil resistance!

Using XL= 2πF.L, we re-arrange to get:
L = XL / (2πF) Assuming F = 50Hz, we get:
L = 63.7kΩ / (2π50) = 202.8H.

Yes, that is over 200 Henries, which is a huge value of inductance. Here is the equivalent circuit of your relay coil, note that the connection between R1 & L1 is simply not accessible to the outside world:

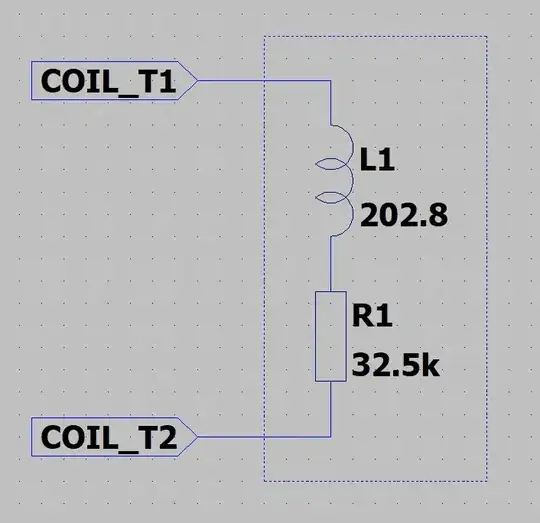
Out of interest, the time constant of the series L & R is:
Tau = L / R
= 202.8H / 32.5kΩ
= 6.24ms.
...which is comparable to the period of the excitation (a 50Hz sinewave has a half-period of 10ms), so yes, the inductance will indeed have a significant effect for the use-case of this load, so it must be taken into consideration in the design process - it cannot be ignored.

Answer 2

The circuit does not need a snubber across the MOC3063. It should be removed.

Snubbers are for suppressing high voltages across mechanical switching contacts that might damage those contacts. You haven't got any mechanical switching contacts. Your switch is a solid-state MOC3063 that switches cleanly and with zero-crossing switch-on. So nothing to suppress.

Incidentally, the MOC3063 is a triac driver and not intended for loads like a relay coil. That doesn't mean it won't work. But its datasheet is clear and explicit on this:

Description The MOC306XM and MOC316XM devices consist of a GaAs infrared emitting diode optically coupled to a monolithic silicon detector performing the function of a zero voltage crossing bilateral triac driver. They are designed for use with a triac in the interface of logic systems to equipment powered from 115/240 VAC lines, such as solid−state relays, industrial controls, motors, solenoids and consumer appliances, etc.

Answer 3

R1 and C1 help to reduce the maximum voltage rise of a reactive load (like your relay = coil) see here.

But your relay has 32500 Ohm and switches off below 34.5 VAC and on beyond 172.5 VAC. In your circuit the relay together with C1 = 100 nF, it forms an R (32kOhm) in series with 100 nF (C1) (R1 negligable), what gives a cutoff frequency of 50 Hz! So the voltage over the relay is 0.7 times 230 = 160 VAC -> so the relay does not switch on (or some few examples). But if the relay is switched on once by the triac - and the triac is switched off, then the C1 keeps the relay at about 160 VAC, that is far above of 34.5 VAC, where it would switch off. That causes the "latch" effect you are saying.

With C1 10 nF the 160 VAC drops to lower voltage, where it is probably at the tolerance of the switching off voltage of 34.5 VAC or higher.

If you remove R1 and C1 - it seams to work, but the inductance part inside the relay could cause the triac to:

• either go beyond its maximum voltage, that is allowed, destroying the triac fast...slowly
• or its dV/dt (commutating voltage) is beyond the limit of the triac (600 or 1000 V/us)

@Spehro Pefhany's idea could work, but it does not hinder the commutating voltage in all cases (especially if 230 VAC supply is switched on).

I am not the specialist, how to calculate the snubber R1 and C1. So the maximum current in the coil of the relay is less than 322 Vp (230 VAC) divided by 32.5 kOhm = ca. 10 mA. You use the MOC3063 with 600 V/us commutating voltage -> a 100 nF capacitor charged with 10 mA increases its voltage with (UC=It) I/C = U/t = 100kV/s = 0.1 V/us -> 6000 times bigger than the limit.

So I would choose 1 nF (100 times smaller), it would give 10 V/us = ok. What about voltage across relay after switching off the triac: C1 = 1 nF -> Xc = 1 / (2 * PI * f * C) = 1 / (2 * PI * 50Hz * 1nF) = 3.18 (j) MOhm -> this is about 100 times higher than the 32.5 kOhm of the relay. So the voltage will be around 2...3 VAC over the relay after the triac switched off. Therefore the relay will drop the contact (2...3 VAC is below 34.5 VAC).

So I think R1 = 1 nF is a good choice - can someone familiar with snubber calculation confirm ... deny my choice?