What is the direct coupling problem which differential amplifiers help avert?

Question

The discussion below comes from Chapter 3.5 of Analysis and Design of Analog Integrated Circuits by Gray, Hurst, Meyer, and Lewis.

In particular, I do not follow what is meant when they write

This property allows direct coupling of cascaded stages without offsets.

I understand the property, but I do not understand why the property allows direct coupling of consecutive stages. Perhaps someone can provide an example that might show how a regular (?) stage does not allow for direct coupling but a differential stage does?

Readers may find this other question a useful contrast: https://electronics.stackexchange.com/questions/698547/what-is-the-problem-with-directly-coupled-amplifiers — Tim Williams, Jan 26 '24 at 08:24

Andy aka · Accepted Answer · 2023-11-28T14:37:46.567

1

Because a decently designed differential amplifier will have very little (or near-zero) common-mode gain (irrespective of a high differential gain), you can attach the differential outputs from one stage to another differential stage's inputs without great worries of the 2nd stage transistors becoming saturated.

This can only happen with differential stages because the common-mode gain is near-zero. A non-differential input has only gain and cannot benefit from any common-mode cancellation.

For instance, imagine a single-ended amplifier with a gain of ten having a nominal output voltage of half the supply rails when the input is 0 volts. You could not connect this directly to another similar stage because that extra stage wants to see 0 volts as a neutral input but, the first stage is supplying it with 6 volts. In other words it would hit the end-stops.

On the other hand you could engineer a single-ended input that produced 0 volts out with 0 volts in then, you could cascade multiple stages but, you then introduce a problem hidden in the first example; your common 0 volt line is likely subject to all sorts of noise currents from other parts of the circuit and, the final result would be a noisy output.

Not so with differential (and impedance balanced) circuits; using differential signal lines means no shared noise with other system components and, any noise that does come along (such as EMI) would affect both simultaneously and, because the CM gain is near-zero, that noise would hardly influence the output differential voltage.

edited Nov 28 '23 at 14:37

answered Nov 28 '23 at 13:40

Andy aka

456,226
28
367
807

1

I am still not sure I see, and perhaps that's because I don't follow what would go wrong if we simply cascaded non-differential (is this the term?) amplifiers. What goes wrong if I directly couple non-differential amplifiers? Are you saying that spurious sources (which I think are what generate common mode gain?) would add on the output to signal gain and then put the input to the next amplifier out of its linear range of operation (is this what you mean by saturate?)?... – EE18 Nov 28 '23 at 14:14
1

...While in contrast, going differentially means that (if we have little common mode gain) then we'll only have signal gain and thus won't have this issue? – EE18 Nov 28 '23 at 14:14
Correct @EE18. I'll try and show an example regarding your first comment.... – Andy aka Nov 28 '23 at 14:27
Just returning here in light of this question (electronics.stackexchange.com/questions/698547/…) as well as a reread of the given section from Gray and Hurst. I think in retrospect I somewhat missed your initial point which is crucial, as given by you in your line "You could not connect this directly to another similar stage because that extra stage wants to see 0 volts as a neutral input...." I guess the initial point you're making here is that, with direct coupling (as is the case here), if a previous stage's biasing does not match up with our stage of interest's biasing then, in effect... – EE18 Jan 29 '24 at 21:04
...we will have some direct current current flowing between the stages at worst or, at best, the given stage of interest will see this delta in biasing at the input as a signal input which will, as you say, cause that stage to "hit the end-stops." The crucial property of the differential amplifier of sufficient symmetry is that if it is biased with $V_{id} = 0$ then its output will have $V_{od} = 0$. If this output is in turn used as the bias for a subsequent differential stage then we have $V_{id} = 0$ for that stage, as is ideal. – EE18 Jan 29 '24 at 21:07
1

As you further point out, in a single-ended directly-coupled arrangement, even if we could arrange for perfectly equal output bias voltage of one stage with input bias voltage of the next, slight noise sources would be propagated and cause potential hitting of end stops. In contrast, I guess our hope with differential circuits is that even if noise arises, it arises equally on each input so that no noise is propagated. This second property is referenced in the opening paragraph to Chapter 3.5 of the text (for posterity and my future reference!) along with the biasing problem alluded to above. – EE18 Jan 29 '24 at 21:09
@EE18 see this also also. It's all about balancing impedances so that noise affects both wires the same. – Andy aka Jan 29 '24 at 21:31
Awesome, thank you Andy! – EE18 Jan 29 '24 at 21:35

Circuit fantasist · Answer 2 · 2024-01-28T11:31:53.013

Basic idea

Single-ended configuration

In direct-coupled amplifier stages, the output voltage of the previous stage is a sum of the amplified AC voltage and the quiescent DC voltage. This composite AC+DC output voltage should be “shifted down” almost to ground level so that the input voltage of the next stage “wiggles” around the zero level. This actually means that a DC voltage equal to the quiescent DC voltage must be subtracted from the composite AC+DC output voltage so that only the AC voltage remains.

Also, under the influence of temperature, the quiescent output voltage and the shifting voltage slightly vary. To be compensated, these changes must be equal and opposite. But in this “single-ended configuration” the two voltages are not under the same conditions - the output voltage is referenced to ground and the shifting voltage is floating; this makes compensation difficult.

Differential configuration

In contrast to the single-ended configuration, here, to make perfect compensation, the two DC voltages are exactly the same and both referenced to ground. However, the resulting AC voltage is "floating" and requires a differential input to the next stage. Note that the “shifting" DC voltage is introduced by another input voltage source which determines the behavior of the former.

Figuratively speaking, in common mode the differential stage “lifts" its internal ground (the common emitter point) to the level of the two output voltages of the previous stage, and in differential mode, these voltages "wiggle" around this "shifted ground". So, the clever trick on which the differential amplifier is based is that in common mode its "internal ground" is not fixed but "movable", following.

Conceptual circuits

We can illustrate the ideas above using simple equivalent electrical circuits.

Immovable real ground

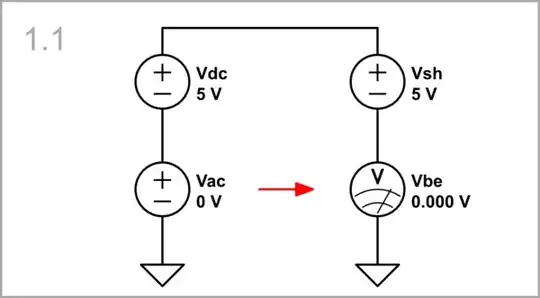
Let's first consider cascading two single-ended stages. The output of the previous stage is represented as two voltage sources (5 V quiescent voltage Vdc and input voltage Vac), connected in series. The "shifting" voltage source Vsh is connected oppositely and in series to Vdc so that its voltage is subtracted. The resulting voltage appears across the voltmeter Vbe (its voltage is decreased to 1 kΩ to roughly resemble a base-emitter junction).

Vac = 0: In the initial case, Vsh compensates Vdc, and the Vac zero voltage appears across Vbe.

schematic

^{simulate this circuit – Schematic created using CircuitLab}

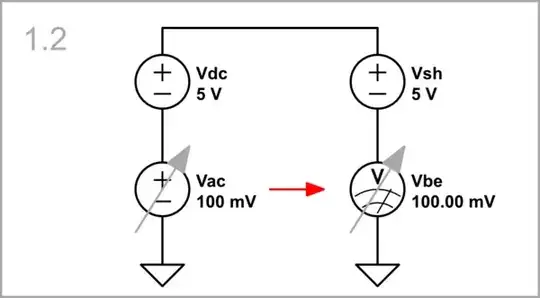
Vac = 100 mV: When Vac slightly increases above Vdc...

schematic

^{simulate this circuit}

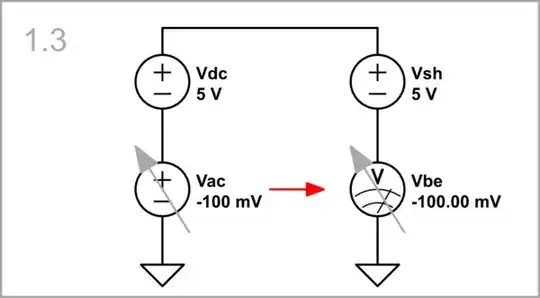
Vac = -100 mV: ... or decreases below Vdc...

schematic

^{simulate this circuit}

... its variations appear shifted down across Vbe (Vac "wiggles" around ground).

The disadvantage of this single-ended DC coupling is that the Vdc and Vsh variations act as an input signal and are amplified by the next stage (try it by slightly changing Vdc and Vsh, and looking at Vbe). Let's see how we can solve this problem.

Immovable virtual ground

With the same success we can put Vsh below Vbe instead above (i.e. to attach it to the next stage). It actually means to "lift" the ground with Vdc.

Vac = 0, Vmg = 5 V: If we keep the movable ground constant (Vmg = Vdc = 5 V)...

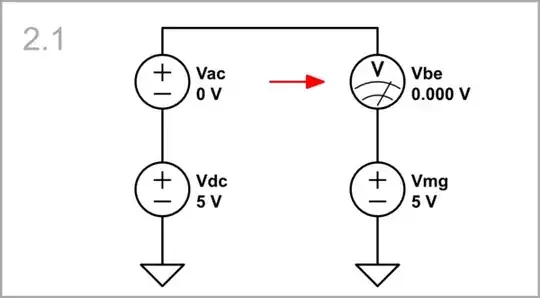
schematic

^{simulate this circuit}

Vac = 100 mV, Vmg = 5 V: ... and increase Vac...

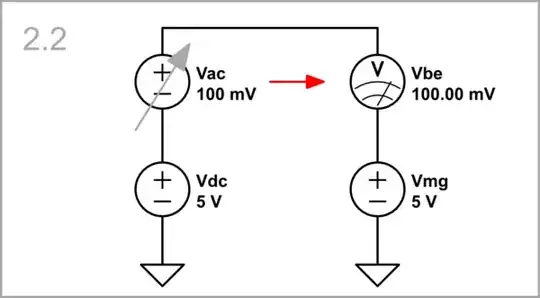
schematic

^{simulate this circuit}

Vac = -100 mV, Vmg = 5 V: ... or decrease Vac...

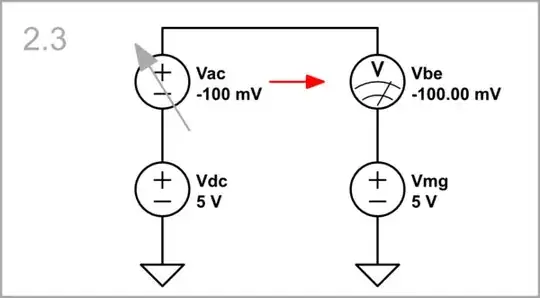
schematic

^{simulate this circuit}

... the result is the same - the Vac variations appear across Vbe. This mode corresponds to the differential mode of the differential amplifier.

Movable virtual ground

But if we move the ground in the same direction...

Vac = 100 mV, Vmg = 5.1 V: ... simultaneously increasing both Vac and Vmg...

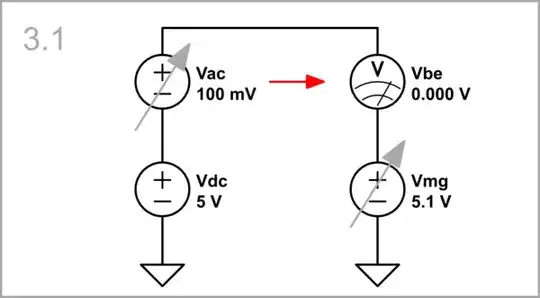
schematic

^{simulate this circuit}

Vac = -100 mV, Vmg = 4.9 V: ... or decreasing them...

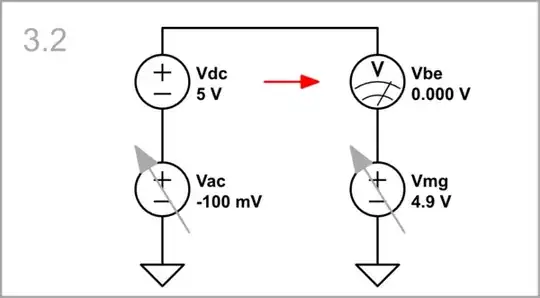
schematic

^{simulate this circuit}

... the result is the same - Vbe = 0 V. This mode corresponds to the common mode of the differential amplifier.

But what is the advantage of this way of coupling amplifier stages? To answer this question, let's see how the "movable ground" is implemented in differential amplifiers.

Movable ground implementation

This "long-tailed pair" arrangement consists of three "sources" in parallel - two (input) voltage sources V1 and V2, and a current source I. For our purposes, we can ignore the current source and focus only on the two voltage sources. So this differential configuration is doubled compared to the single-ended configuration above.

Movable ground: If the two input voltages change in the same way (common mode), the midpoint FG will also change this way, and will act as a "following movable ground".

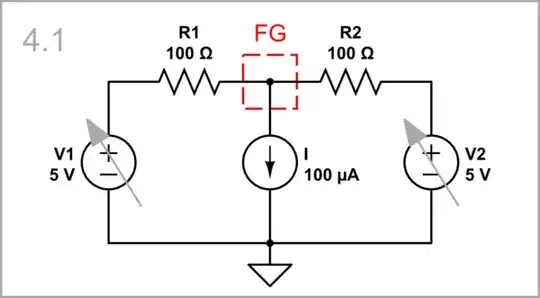
schematic

^{simulate this circuit}

Fixed ground: If the two input voltages change in the opposite directions (differential mode), the VG midpoint voltage will not change, and will act as a "virtual ground".

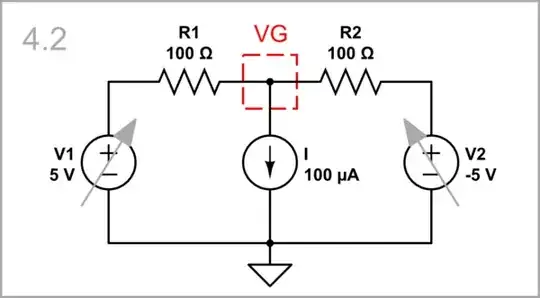
schematic

^{simulate this circuit}

So the mechanism of this differential coupling is as follows: When V1 = V2, the "movable virtual ground" moves freely to the Vdc level, and when V1 = -V2, it is fixed there. Its advantage is that the "movable ground" is automatically set equal to the input DC voltage and will move when it varies due to temperature for example.

Practical circuit

This concept can be seen in the practical circuit of the transistor differential amplifier below. The previous stage is simplified and split into two halves, and they are placed on either side of the next step.

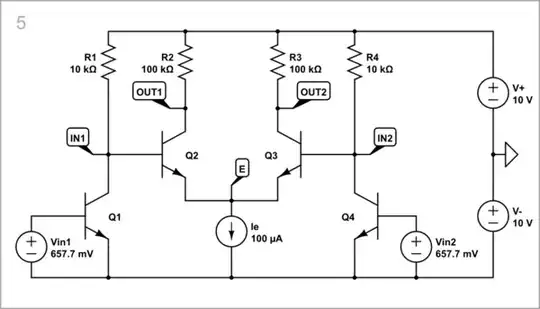
schematic

^{simulate this circuit}

You can conduct the conceptual experiments above by this practical circuit.

Conclusion

DC amplifiers are made by cascading differential amplifier stages because their input voltages are referenced to a movable internal ground which follows the input quiescent voltages.

Thank you so much for this wonderful answer. I am not sure I totally understand everything and partially that's because I'm not yet (back) at differential circuits in my text (hoping to get there in next couple days), at which point hopefully I will understand this better. For now, I just have one question if it's OK: — EE18, Jan 28 '24 at 00:52
“The disadvantage of this single-ended DC coupling is that the Vdc and Vsh variations act as an input signal and are amplified by the next stage (try it by slightly changing Vdc and Vsh, and looking at Vbe).” What do we mean by “act as an input signal” here? Is the point that both Vdc and Vsh are set by the respective bias circuits of the two stages and so may change for whatever reason, and so if they differ then we will be putting a DC) signal on top of Vac (Vac may or may not be DC)? — EE18, Jan 28 '24 at 00:52
Also, to confirm, it seems sometimes you use DC to mean "direct current" and other times "directly-coupled", right? — EE18, Jan 28 '24 at 00:53
Also (another also!), should the V1 and V2 in your differential pair experiments be thought of as analogous to your Vdc with a movable ground in the case when V1 = V2, and thought of as analogous to Vdc with an immovable ground in the case when V1 = -V2? — EE18, Jan 28 '24 at 00:56
@EE18, Regarding question 1: The output voltage of an amplifier is actually a function of many quantities (input voltages, other voltages, resistances, gains, etc.) but we only consider one or two of them useful and want the amplifier to respond to their change. We consider the rest to be harmful and we try our best that the amplifier does not "pay attention" to their change. In this case, Vdc and Vsh must remain constant (after we have set them once) for only Vin to act. But a clever idea would be to vary them oppositely so as to neutralize each other's changes. — Circuit fantasist, Jan 28 '24 at 11:08
@EE18, In a DC amplifier, Vac can be any voltage - slowly changing (DC), periodic with respect to zero (AC), sinusoidal or of any shape. The transistor collector voltage is a changing (between 0 and Vcc ) voltage that we can think of as composed of a constant voltage Vdc (set by the bias circuit) and a changing voltage Vac. Of course, as you suggest, we can represent the variations of Vdc and Vsh as additional varying voltages. According to me, "DC" means "constant" or better "slowly changing voltage". "DC- coupled" means "connected through elements having constant voltage across themselves". — Circuit fantasist, Jan 28 '24 at 11:26
@EE18, About your last comment: Exactly! I have first introduced the idea of the "shifting virtual ground" in the single-ended stage (schematics 2.1 ÷ 3.2) and then shown how it is implemented "doubled" in the differential stage (schematics 4.1, 4.2 and 5). In the latter, the two voltages Vdc(1) and Vsh (Vdc2) are fully symmetrical and grounded, and therefore fully compensated. It might be good to ask another question specifically about the (great) idea of the differential stage (the so-called "long-tailed pair"). — Circuit fantasist, Jan 28 '24 at 11:53
Just a comment as I read through this lovely answer again (I am now back into the differential pairs section of my text). You write "This composite AC+DC output voltage should be “shifted down” almost to ground level so that the input voltage of the next stage “wiggles” around the zero level" and my question is whether you really mean the zero level or, rather, "the input bias voltage (whatever is optimal for design) for the next stage" which, in general, is nonzero? — EE18, Jan 29 '24 at 21:13
@EE18, Just to mention first that I'm nearing the end of the other story and will finish it soon. Your remark is very accurate, but here, for the sake of simplicity, I have assumed that the input of the next stage is 0 V ("ideal" transistor with zero Vbe) and represented it with a 1 kΩ voltmeter. It could also be represented with an ammeter with a resistance of the order of several hundred ohms or even assumed to be a short circuit and in practice controlled by current. A separate question can be devoted to how the BJT input behaves, but if you want, we can continue to discuss it here. — Circuit fantasist, Jan 30 '24 at 13:58
@EE18, Unfortunately there is some problem uploading the images because I keep getting the message "failed to upload the schematic image". I hope it is temporary. — Circuit fantasist, Jan 30 '24 at 14:58

What is the direct coupling problem which differential amplifiers help avert?

2 Answers2

Basic idea

Single-ended configuration

Differential configuration

Conceptual circuits

Immovable real ground

Immovable virtual ground

Movable virtual ground

Movable ground implementation

Practical circuit

Conclusion

Linked