Comparator with hysteresis equation for Vmax Vmin

Question

In a scientific paper (Design Considerations for Current Transformer Based Energy Harvesting for Electronics Attached to Electric Motor J. Ahola et. al.) I came across the comparator circuit with hysteresis shown in the picture. The authors of the paper use this circuit to control the voltage at a capacitor. If the voltage at the capacitor exceeds a level Vdc,max the comparator should output high, if the voltage falls below the level Vdc,min the comparator should output low. The reference voltage of the comparator is set with Zener diode D3. R3 is used to limit the current through the Zener diode. I would now like to derive the equations for Vdc,min and Vdc,max given in the paper myself but fail at times.

As a first approach I tried to solve it using the voltage divider approach as soon as the voltage at the positive input is greater than Vz the comparator should switch, before that the output must be at Vcc-Low = GND. Therefore the voltage at R2 has to be determined. is this the right approach?

Answer 1

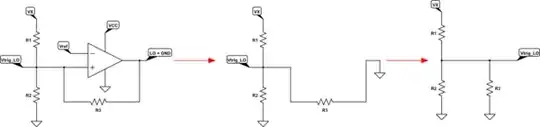
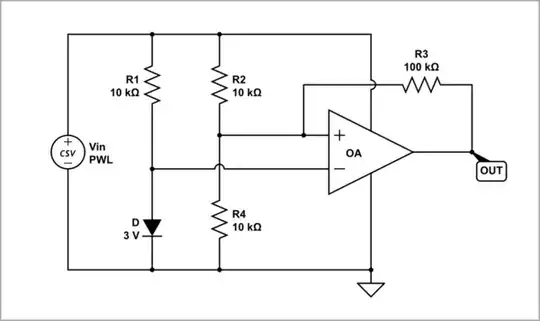
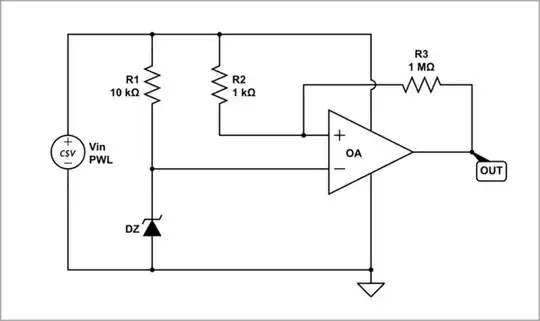
This is how I would approach the problem. Below is the circuit drawn with nodes Z and X, where Z has fixed reference potential \$V_Z\$, and X has potential \$V_X\$ that is a function of both output \$V_{OUT}\$ and the supply \$V_{DC}\$:

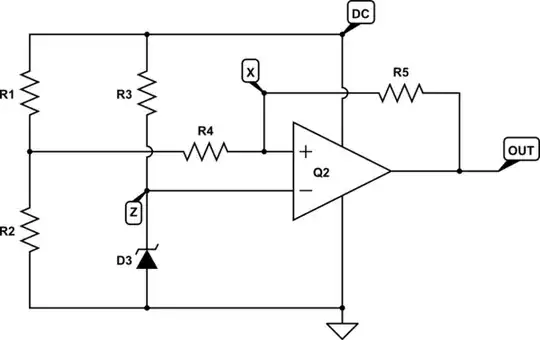
^{simulate this circuit – Schematic created using CircuitLab}

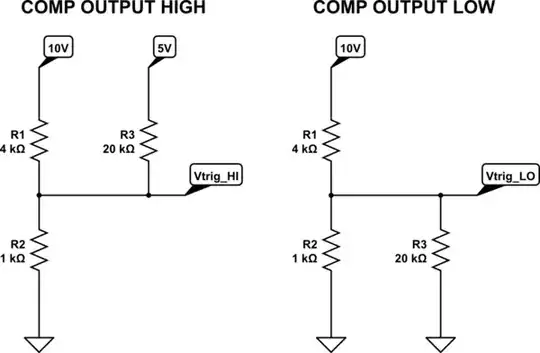
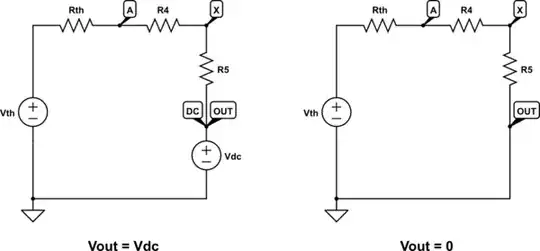
You have two conditions to consider, output high, \$V_{OUT} = V_{DC}\$, and low, \$V_{OUT} = 0V\$. In the former case, we have a network of resistances connected as shown below left, and the latter situation on the right:

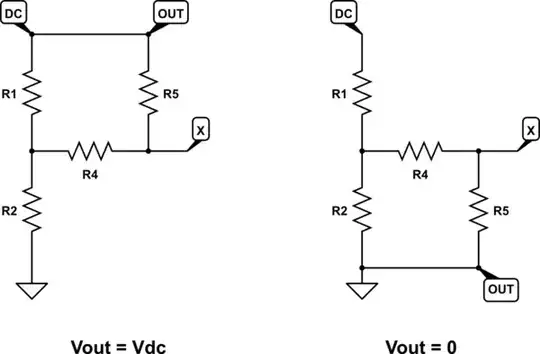
^{simulate this circuit}

The algebra is easier if we treat the supply DC and resistors R1 and R2 as their Thevenin equivalent:

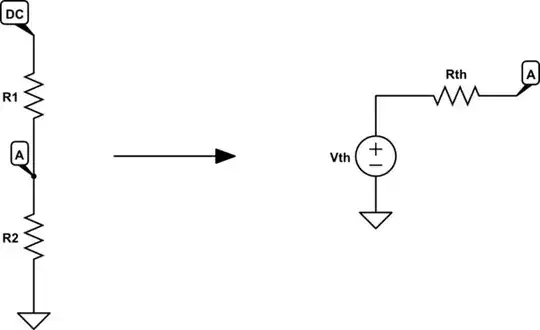
^{simulate this circuit}

where:

$$ V_{TH} = V_{DC}\frac{R_2}{R_1+R_2} $$

$$ R_{TH} = R_1 \parallel R_2 = \frac{R_1R_2}{R_1 + R_2} $$

The resistor networks in each situation (high and low output) are therefore equivalent to these:

^{simulate this circuit}

These are simple resistor potential dividers, the only difference between the two being the presence/absence of the voltage source \$V_{DC}\$. The potentials at X are trivial to write:

$$ V_{X(H)} = V_{DC} + (V_{TH} - V_{DC})\frac{R_5}{R_4 + R_5 + R_{TH}} $$

$$ V_{X(L)} = V_{TH}\frac{R_5}{R_4 + R_5 + R_{TH}} $$

You may have noticed that R4 is redundant. It's effectively in series with the other two resistances R5 and Rth. You can obtain exactly the same values for \$V_X\$, in both states, by removing it altogether, and adjusting Rth and/or R5 to compensate. I won't do that here, it's just a heads-up.

Now you can substitute back in the expressions for \$V_{TH}\$ and \$R_{TH}\$ from before. The last step is to equate \$V_{X(H)} = V_Z\$ and \$V_{X(L)} = V_Z\$, which I think you can handle from here. You should end up with expressions for \$V_{X(H)}\$ and \$V_{X(L)}\$ in terms of only the resistances and \$V_{DC}\$.

---

Update 1 - choosing resistances

Here's an answer I wrote about this, which will help to choose an order of magnitude for the resistances in the circuit.

If you start by specifying explicit potentials for the upper and lower switching thresholds, say \$V_{DC}=8V\$ and \$V_{DC}=6V\$, and the zener voltage, say \$V_Z=4.7V\$, you obtain two simultaneous equations that can be rearranged to yield any two of the resistances. The problem is that there are four resistances to find, and only two simultaneous equations. That's because there are infinitely many solutions for those resistances that would satisfy the conditions described by the equations.

_{Note: As I mentioned before, I consider \$R_4\$ and \$R_{TH}\$ to be a single resistance, and it will greatly simplify things if you set \$R_4 = 0\Omega\$. You could always re-introduce \$R_4\$ again later, and adjust \$R_{TH}\$ to compensate, but I see no reason to do that. \$R_4\$ is completely redundant here.}

It seems impossible to solve, but all you need to do is randomly (well, not randomly, follow the guidelines from the linked answer above) select values for any two of them, say \$R_4 = 10k\Omega\$ and \$R_5=100k\Omega\$, and then solve for the other two.

At this stage it doesn't matter whether you guessed those resistances correctly or not, because the ratio of the resistances will be the same for all solutions. That is, if you multiply all the resistances by the same factor (say 2, or 0.5) they will still be valid solutions, and the thresholds remain the same. This is due to the linear nature of the system.

So if, for example, when you solve the system of equations using some randomly chosen value of R4 and R5 (or any of them), but you find the resulting resistances to be on the low side, then double them all (or multiply them all by whatever factor would yield more appropriate values), and they will produce the same voltages everywhere. This trick wouldn't work if the equations weren't linear, but in this case they are.

---

Update 2 - a walkthrough

$$ V_{X(H)} = V_{DC} + (V_{TH} - V_{DC})\frac{R_5}{R_4 + R_5 + R_{TH}} $$

$$ V_{X(L)} = V_{TH}\frac{R_5}{R_4 + R_5 + R_{TH}} $$

The Thevenin equivalencies:

$$ V_{TH} = V_{DC}\frac{R_2}{R_1+R_2} $$

$$ R_{TH} = \frac{R_1R_2}{R_1 + R_2} $$

Combining these:

$$ \begin{aligned} V_{X(H)} &= V_{DC} + \left( V_{DC}\frac{R_2}{R_1+R_2} - V_{DC} \right) \frac{R_5}{R_4 + R_5 + \frac{R_1R_2}{R_1 + R_2}} \\ \\ &= V_{DC} \left( 1 - \frac{R_1R_5}{(R_4+R_5)(R_1+R_2)+R_1R_2} \right) \\ \\ \\ \\ V_{X(L)} &= V_{DC} \left( \frac{R_2}{R_1+R_2} \right) \left( \frac{R_5}{R_4 + R_5 + \frac{R_1R_2}{R_1 + R_2}} \right) \\ \\ &= V_{DC} \frac{R_2R_5}{(R_4+R_5)(R_1+R_2)+R_1R_2} \\ \\ \end{aligned} $$

We are going to specify values of \$V_{DC}\$ where we intend switching to occur, corresponding to when \$V_X=V_Z\$ in each case, so substitute \$V_X\$ with \$V_Z\$:

_{Note: counter-intuitively, the upper threshold \$V_{DC(MAX)}\$ occurs when the output is low, and vice versa.}

When the output is high:

$$ \begin{aligned} V_Z &= V_{DC(MIN)} \left( 1 - \frac{R_1R_5}{(R_4+R_5)(R_1+R_2)+R_1R_2} \right) \\ \\ V_{DC(MIN)} &= V_Z \frac{(R_4+R_5)(R_1+R_2)+R_1R_2}{(R_4+R_5)(R_1+R_2)+R_1R_2-R_1R_5} \\ \\ \end{aligned} $$

When the output is low:

$$ \begin{aligned} V_Z &= V_{DC(MAX)} \frac{R_2R_5}{(R_4+R_5)(R_1+R_2)+R_1R_2} \\ \\ V_{DC(MAX)} &= V_Z \frac{(R_4+R_5)(R_1+R_2)+R_1R_2}{R_2R_5} \\ \\ \end{aligned} $$

These don't look much like the equations quoted in your question. I don't want to spend ages reconciling your equations with mine. In any case, mine here are correct.

Since both of these share the same rather complex term, I'll write them like this:

$$ \begin{aligned} K &= (R_4+R_5)(R_1+R_2)+R_1R_2 \\ \\ V_{DC(MIN)} &= V_Z \frac{K}{K-R_1R_5} \\ \\ V_{DC(MAX)} &= V_Z \frac{K}{R_2R_5} \\ \\ \end{aligned} $$

Let's establish some targets. These are some example characteristics I am aiming for, using a 4.7V zener diode:

$$ \begin{aligned} V_Z &= 4.7V \\ \\ V_{DC(MIN)} &= 6V \\ \\ V_{DC(MAX)} &= 8V \\ \\ \end{aligned} $$

Unfortunately, here's where things get difficult, because to solve these two equations with four unknown resistances, requires us to "guess" two of them. If we choose unwisely the equations could yield a solution for the other two with negative resistances. Algebraically the solution would still be valid, but physically impossible to build.

Intuitively, I see that \$R_5\$ and \$R_4\$ together are responsible for hysteresis, the "gap" between the two thresholds. \$R_1\$ and \$R_2\$ on the other hand control the "midpoint" potential. We would have to take great care when setting the midpoint, which would be algebraically complicated, so I won't specify \$R_1\$ or \$R_2\$. I'd rather let the algebra we've already established deal with that.

Instead, I'll try choosing arbitrary values for \$R_4\$ and \$R_5\$. I am sure that \$R_4=0\$ will work just fine (which I recommend), but in the interest of keeping \$R_4\$ in this design, I'm going to set it to be much smaller than \$R_5\$, and non-zero. If \$R_4\$ is too large compared with \$R_5\$, we may inadvertently make it impossible for \$V_X\$ to ever equal \$V_Z\$, which would yield negative \$R_1\$ and/or \$R_2\$ in the solution.

$$ \begin{aligned} R_4 &= 10\Omega \\ \\ R_5 &= 100\Omega \\ \\ \end{aligned} $$

Clearly, those values are too small, but they keep the calculations simple, and permit me to show you later on how we can adjust and correct them.

Plug these values into the simultaneous equations from above:

$$ \begin{aligned} K &= (R_4+R_5)(R_1+R_2)+R_1R_2 \\ \\ &= 110(R_1+R_2)+R_1R_2 \\ \\ \end{aligned} $$

$$ \begin{aligned} V_{DC(MIN)} &= V_Z \frac{K}{K-R_1R_5} \\ \\ 6 &= 4.7 \frac{K}{K-100R_1} \\ \\ R_1 &= \frac{1.3}{600}K \\ \\ \end{aligned} $$

$$ \begin{aligned} V_{DC(MAX)} &= V_Z \frac{K}{R_2R_5} \\ \\ 8 &= 4.7 \frac{K}{100R_2} \\ \\ R_2 &= \frac{4.7}{800}K \\ \\ \end{aligned} $$

To solve these, substitute the expressions for \$R_1\$ and \$R_2\$ into the equation for \$K\$, and solve for \$K\$. Then use that value for \$K\$ to evaluate \$R_1\$ and \$R_2\$. We finally have all resistances:

$$ \begin{aligned} R_1 &= 19.57\Omega \\ \\ R_2 &= 53.07\Omega \\ \\ R_4 &= 10\Omega \\ \\ R_5 &= 100\Omega \\ \\ \end{aligned} $$

These are far too small, and will draw too much current from the supply and op-amp output. With these equations all being linear, we can simply scale all resistances by the same factor, without changing any voltages anywhere.

This means you can find a factor that will adjust any one of the resistances to become any value you choose, and when you scale all the resistances by that same factor, circuit behaviour doesn't change. I will multiply them all by 1000, to get resistances in the tens of kilohms:

$$ \begin{aligned} R_1 &= 19.57k\Omega \\ \\ R_2 &= 53.07k\Omega \\ \\ R_4 &= 10k\Omega \\ \\ R_5 &= 100k\Omega \\ \\ \end{aligned} $$

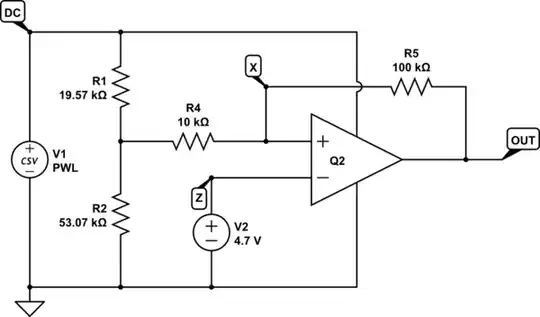
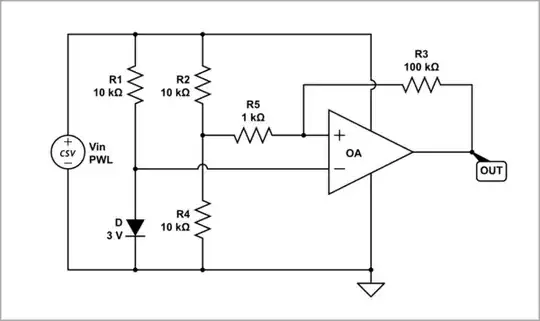
^{simulate this circuit}

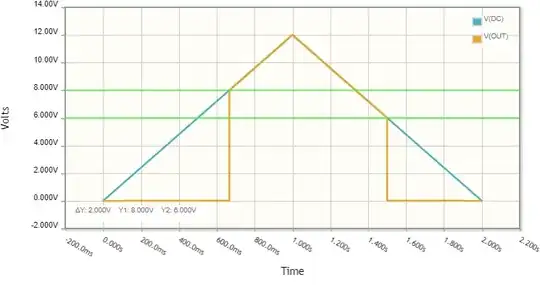
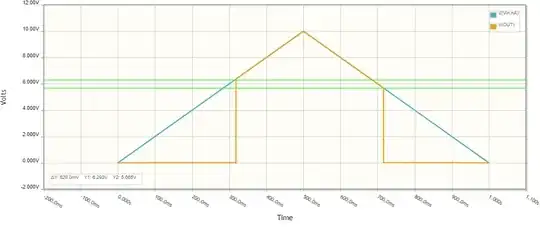
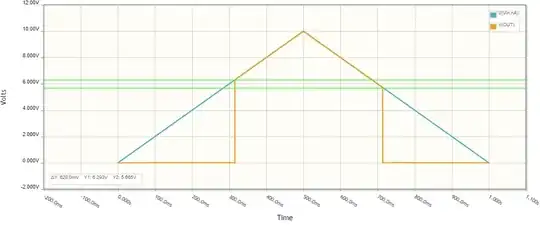
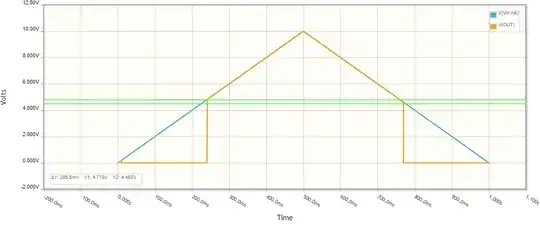
Here's a plot of \$V_{DC}\$ and \$V_{OUT}\$ as I sweep V1 from 0V to 12V and back to 0V. As you can see, the output rises when \$V_{DC}=8V\$, and falls again when \$V_{DC}=6V\$:

Answer 2

If the voltage at the capacitor exceeds a level Vdc,max the comparator should output high, if the voltage falls below the level Vdc,min the comparator should output low.

The comparator with hysteresis may not be a solution to your problem. Because with hysteresis, the max and min points change slightly around the original reference point (the reference without the hysteresis).

So window comparator might be what you need:

---

If the comparator with hysteresis what you need, here's your answer:

is this the right approach?

I couldn't understand your approach but here's how I calculate:

Without the extra resistor (from output to non-inverting input) the trigger point would be the reference voltage (voltage at the inverting input). Quite simple:

^{simulate this circuit – Schematic created using CircuitLab}

With the extra resistor the division ratios will change. Assume the comparator gave an output of HI (VCC):

^{simulate this circuit}

So if you calculate Vtrig_HI from the divider network above that'll be the max trigger point.

Likewise, assume the comparator gave an output of LO (GND):

^{simulate this circuit}

Again, if you calculate Vtrig_LO from the divider network above that'll give you the min trigger point.

---

EXAMPLE:

VX = 10V, R1 = 10k, R2 = 1k, and comparator's supply is VCC = 5V.

Without any hysteresis the trigger point would be 2V.

But if we add an extra resistance of R3 = 20k for hysteresis, using the two diagrams above, the low trigger would be 1.92V and the high trigger would be 2.11V.

^{simulate this circuit}

For HI, solve the following for Vtrig-HI:

$$ \mathrm{ \frac{10V-V_{trig-HI}}{4k}+\frac{5V-V_{trig-HI}}{20k}=\frac{V_{trig-HI}}{1k} } $$

And for LO, solve the following for Vtrig-LO:

$$ \mathrm{ V_{trig-LO} = 10V \cdot \frac{(1k \ || \ 20k)}{4k+(1k \ || \ 20k)} } $$

---

You can derive the equations if you want. During a design, I normally put the calculations into an Excel file and play with the values (cells) to see how trigger points change.

Answer 3

One way to immediately write down the answer is to do a Wye-Delta transformation on R1, R2, R4.

Then (picking the more complex one, because why not) we can immediately write:

\$ \frac{V_{MIN}}{V_Z} = \frac{R_5 ||R_{AC}}{R_{BC}} +1 \$

where \$R_{AC} = \frac{R_1 R_2 + R_1 R_4 + R_2 R_4}{R_2}\$ and \$R_{BC} = \frac{R_1 R_2 + R_1 R_4 + R_2 R_4}{R_1}\$

A bit of manipulation later and you'll see that the authors of the paper missed an added R1*R2 in both numerator and denominator, which might explain why you are having problems deriving their equation.

I'll leave the other derivation to you.

Answer 4

Looking for the minimalistic solution...

This "scientific solution" caught my attention firstly with its many resistors, secondly with its single power supply, thirdly with the fact that the input signal serves as a power supply, and finally with the strange shape of its output signal which follows the input. I instinctively felt that it could be simplified and felt the desire to do so, albeit with less than "scientific methods". In the end, I was able to reduce the number of resistors by two. Here is how I did it.

5-resistor solution

In the original OP solution, the input voltage is scaled down twice with a voltage divider R2-R4 and applied to the input of a non-inverting comparator with hysteresis. Through the voltage divider R5-R3, a positive feedback is realized through which the hysteresis is obtained.

^{simulate this circuit – Schematic created using CircuitLab}

4-resistor solution

If we make the voltage divider R2-R4 high enough resistive, it can also perform the functions of the input resistor R5; so we can remove the latter.

^{simulate this circuit}

3-resistor solution

And finally, we can try to assign the functions of the R2-R4 voltage divider to the input resistor R5 (R2 in the schematic below).

^{simulate this circuit}

In my opinion, the circuit should not work at its lower threshold because the reference voltage on the Zener diode ceases to be constant... but the graph shows hysteresis. This mystery should be cleared up...

Conclusion

In general, I think that supplying the op-amp from the input signal is not a good idea.