I am trying to calculate the parameters ζ, Q, Fo, Gain (dB), and BW of this circuit. I am confident in the following equations:
Fo = 1 / (2 * π * √(L2 * C1)) ; Q = 1 / (2 * ζ) ; BW = Fo / Q
R2 = R5; therefore, when the wiper is in the middle position, I know it's an unit gain (-1). However, I am unsure about the equations for ζ and Gain (dB) for the other scenarios.
Could you please assist me with these equations?
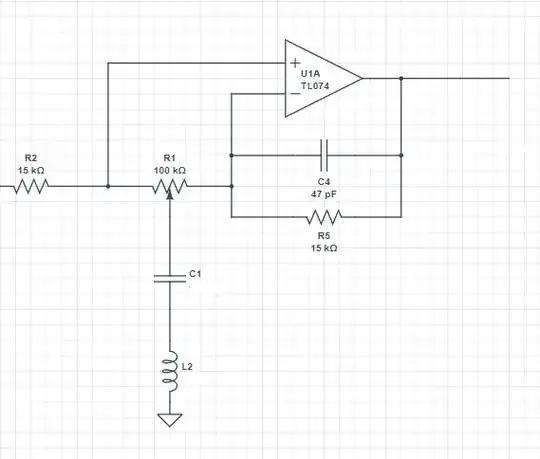
To keep the transfer function 2nd order, \$C_4\$ needs to be ignored. No harm in doing so. (It's there to keep the opamp from oscillating at high frequency and doesn't really serve another purpose here.)
What I find is that the critical frequency is, as you already know, \$\omega_{_0}=\frac1{\sqrt{L_2\,C_1}}\$ or \$f_{_0}=\frac1{2\pi\,\sqrt{L_2\,C_1}}\$.
So nothing new there.
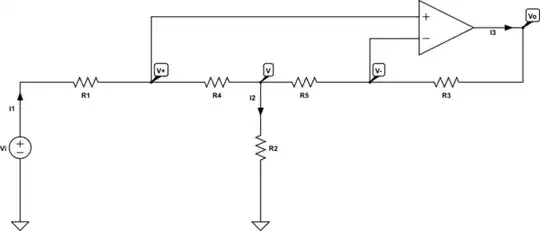
Analysis starts with assigning \$V_x\$ to the wiper point of the potentiometer and then splitting up the potentiometer into two resistor values based upon the wiper position, \$p\$. The following shows how to do it with SymPy/Sage/Python (freely available):
rx1 = p*r1 # left side pot R
rx2 = (1-p)*r1 # right side pot R
ep = Eq( vp/r2 + vp/rx1,vi/r2 + vx/rx1 ) # (+) opamp node KCL
em = Eq( vm/rx2 + vm/r5, vx/rx2 + vo/r5 ) # (-) opamp node KCL
ex = Eq( vx/rx1 + vx/rx2 + vx/(s*l2+1/s/c1), vp/rx1 + vm/rx2 ) # Vx KCL
eo = Eq( vo/r5, io + vm/r5 ) # opamp output node KCL
answer = solve( [ep, em, ex, eo, Eq(vm,vp)], [vm, vp, vo, io, vx] )
tf = tf2( an2[vo] / vi )
{
omega: 1/(sqrt(c1)*sqrt(l2)),
zeta: sqrt(c1)*(-p**2*r1/2 + p*r1/2 - p*r2/2 + r2/2)/sqrt(l2),
P: [{A: 1, N: 2},
{A: p*(p*r1 - r1 - r5)/(p**2*r1 - p*r1 + p*r2 - r2), N: 1},
{A: 1, N: 0}]
}
(tf2 is a function I wrote some time ago. I can provide it, if needed.)
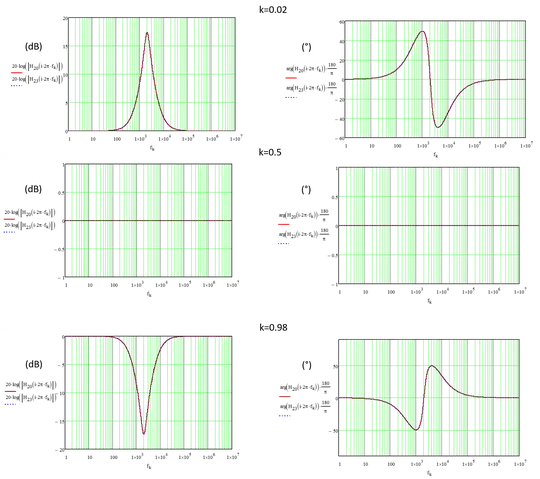
This is an all-pass filter, so it has all three components:
$$\begin{align*} H\left(s\right)&=\underbrace{\overbrace{\left[1\vphantom{\frac{\left(1-p\right)R_1-R_5}{\left(1-p\right)R_1+\left(\frac1{p}-1\right)R_2}}\right]}^{\text{gain}}\cdot\frac{\left(\frac{s}{\omega_{_0}}\right)^2}{\left(\frac{s}{\omega_{_0}}\right)^2+\frac1{Q}\left(\frac{s}{\omega_{_0}}\right)+1}}_{\text{high-pass}} \\\\ & +\underbrace{\overbrace{\left[\frac{\left(1-p\right)\cdot R_1-R_5}{\left(1-p\right)\cdot R_1+\left(\frac1{p}-1\right)\cdot R_2}\right]}^{\text{gain}}\cdot\frac{\frac1{Q}\left(\frac{s}{\omega_{_0}}\right)}{\left(\frac{s}{\omega_{_0}}\right)^2+\frac1{Q}\left(\frac{s}{\omega_{_0}}\right)+1}}_{\text{band-pass}} \\\\ &+\underbrace{\overbrace{\left[1\vphantom{\frac{\left(1-p\right) R_1-R_5}{\left(1-p\right)R_1+\left(\frac1{p}-1\right)R_2}}\right]}^{\text{gain}}\cdot\frac{1}{\left(\frac{s}{\omega_{_0}}\right)^2+\frac1{Q}\left(\frac{s}{\omega_{_0}}\right)+1}}_{\text{low-pass}} \end{align*}$$
Where \$0 \le p \le 1\$ is the potentiometer position with 0 being all the way to the left and 1 being all the way to the right.
What I write below assumes the resistor values you provided. There is enough information here that you can alter those values to see how it impacts things. But I'm not going to complicate what I write by discussing how you might want to change those values, as well. I'll leave that part to you. At least there's info to use in considering how they impact the inductor to capacitor ratios. (They do.)
The midband (where you set \$f_{_0}\$) will have a relative gain of about \$2\$ with \$p\approx 0.888\$ or 88.8% towards the right and a relative gain of about \$\frac12\$ with \$p\approx 0.112\$ or 11.2%. Outside the range between those two positions things start to go rapidly south. So I'd recommend placing the potentiometer between two other resistors in series to keep things reasonable. Perhaps \$6.8\:\text{k}\Omega\$ or thereabouts.
Here, then, also find: \$Q=\frac1{\left(1-p\right)\,\cdot\,\left(R_2+p\,\cdot\, R_1\right)}\cdot \sqrt{\frac{L_2}{C_1}}\$.
This tells you that the range of \$Q\$ is directly proportional to the square-root of the ratio of \$L_2\$ to \$C_1\$.
In fact, your choice of \$f_{_0}\$ and \$Q\$ or \$\zeta\$ (when the potentiometer is at 50%) pretty much determines \$C_1\$ and \$L_1\$. No real choice in the matter.
Assume \$k\$ is a multiplier such that \$L_2=k\cdot C_1\$. Then \$k=\left(Q\cdot\left(1-p\right)\cdot\left(R_2+p\cdot R_1\right)\right)^2\$ and \$C_1=\frac1{2\pi\,f_{_0}\,\sqrt{k}}\$ and \$L_2=\frac{\sqrt{k}}{2\pi\,f_{_0}}\$.
So there's really no choice in values, given some chosen bandwidth (\$Q\$ or \$\zeta\$ determines this, as you already know.) And for a narrow bandwidth (high-\$Q\$) the inductor is going to be very large and the capacitor very small to make it work. (Note also that large inductors will have significant parasitic series resistance that isn't accounted here -- possibly also significant capacitance as well if \$C_1\$ computes out small enough. None of this was included in the analysis here.)
I think this circuit is for more towards the highly-damped cases (wide bandwidth.)
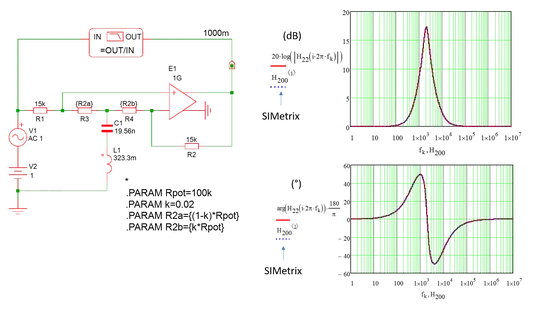
Only after the above analysis did I plug anything into LTspice. (I almost never use LTspice until after I've attempted analysis, first.) And it confirms the above analysis, to the letter!
Let's say \$f_{_0}=2\:\text{kHz}\$ and that \$\zeta=4\$. I'll set the potentiometer to three places, \$p=0.5\$, \$p=0.112\$, and \$p=0.888\$ (we should expect midband gains of about 1, about 1/2, and about 2.)
Here's the run for \$p=0.5\$:
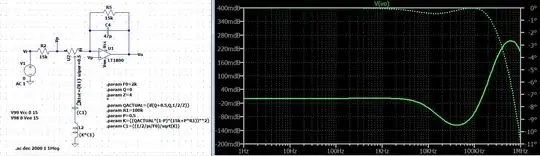
Fairly flat, as expected.
Here's the run for \$p=0.112\$:
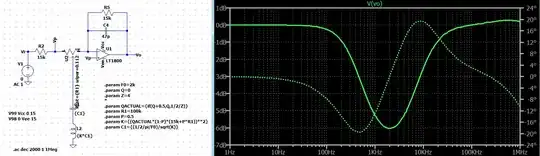
Note that the bottom of the dip is right at \$2\:\text{kHz}\$ and \$-6\:\text{dB}\$. Just as predicted.
Here's the run for \$p=0.888\$:
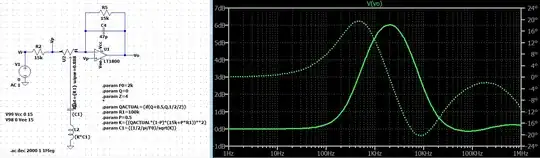
Note that the top of the dip is right at \$2\:\text{kHz}\$ and \$+6\:\text{dB}\$. Also just as predicted.
Just FYI, though? \$C_1=19.59\:\text{nF}\$ and \$L_2=323.3\:\text{mH}\$. Those were computed from the chosen critical frequency and desired damping factor (when the potentiometer is right at midpoint position and given your resistor values, of course.)
(Also, the various non-idealities you see in the curves from about \$100\:\text{kHz}\$ and beyond come largely from \$C_4\$. If I set it close to zero then they go away and the curves look much closer to ideal curves.)
I have looked at this circuit and applied the fast analytical circuits techniques or FACTs. The procedure is not too complicated considering the potentiometer replaced by two resistances in series with the junction corresponding to the wiper: \$R_{2a}=(1-k)R_{pot}\$ and \$R_{2b}=kR_{pot}\$.
You first determine the dc gain \$H_0\$ when the capacitor is open and the inductor shorted. With this particular configuration, \$H_0=1\$. Then you will determine the resistance \$R\$ driving the capacitor and the inductor to obtain their associated time constants: \$\tau_1=RC_1\$ and \$\tau_2=\frac{L_2}{R}\$. Follow the high-frequency gains to express the zeroes and you have the transfer function you need (I purposely ignored the high-frequency pole brought by the 47-pF capacitor):
Below are a few magnitude/phase plots with the wiper in different positions, I used the \$LC\$ values computed by periblepsis:
and, finally, a quick check with a SIMetrix plot imported in Mathcad to compare phase and mag responses with the calculated values:
Could you please assist me with these equations?
Where did the circuit idea come from? Was it a graphic equalizer?
I found this in a text book. It is indeed for a graphic equalizer. – flower.fish
The maximum Q-factor (minimum zeta) is set by the L and the C series resistance when the pot is at either of the extreme positions. This is the important parameter to uncover so, given that your title is thi: -
Analysis of an RCL Filter Utilizing a Potentiometer as R.
........you are missing the point of where the important/relevant zeta is defined. It is not defined by the potentiometer when the wiper is set at the end-points and, this is where you need to define it else, the graphic equalizer won't have the correct bandwidth when fully boosting or fully attenuating the particular band is is tuned to.
Maybe if you read this wiki page on series RLC circuits you can start to figure out what you need formulaically: -
But, I would also encourage you to model the circuit in a simulator so that you can test the effects of the potentiometer boosting or attenuating the particular band.
Well, we have the following OPAMP-circuit:
simulate this circuit – Schematic created using CircuitLab
When we use and apply KCL, we can write the following set of equations:
$$\text{I}_2=\text{I}_1+\text{I}_3\tag1$$
When we use and apply Ohm's law, we can write the following set of equations:
$$ \begin{cases} \begin{alignat*}{1} \text{I}_1&=\frac{\displaystyle\text{V}_\text{i}-\text{V}_+}{\displaystyle\text{R}_1}\\ \\ \text{I}_2&=\frac{\displaystyle\text{V}-0}{\displaystyle\text{R}_2}\\ \\ \text{I}_3&=\frac{\displaystyle\text{V}_\text{o}-\text{V}_-}{\displaystyle\text{R}_3}\\ \\ \text{I}_1&=\frac{\displaystyle\text{V}_+-\text{V}}{\displaystyle\text{R}_4}\\ \\ \text{I}_3&=\frac{\displaystyle\text{V}_--\text{V}}{\displaystyle\text{R}_5} \end{alignat*} \end{cases}\tag2 $$
Now, when working with ideal an OPAMP we know that we can set \$\displaystyle\text{V}_+=\text{V}_-\$. Now, we can solve for the transfer function:
$$\mathscr{H}:=\frac{\displaystyle\text{v}_\text{o}}{\displaystyle\text{v}_\text{i}}=\frac{\displaystyle\text{R}_2\left(\text{R}_4+\text{R}_5\right)+\text{R}_4\left(\text{R}_3+\text{R}_5\right)}{\displaystyle\text{R}_2\text{R}_4+\text{R}_5\left(\text{R}_1+\text{R}_2+\text{R}_4\right)}\tag3$$
Now, applying this to your circuit we need to use the Laplace equivalent of the components, which are:
Where \$\displaystyle\alpha\space\text{||}\space\beta:=\frac{\displaystyle\alpha\beta}{\displaystyle\alpha+\beta}\$.
So, we get:
\begin{equation} \begin{split} \mathscr{H}\left(\text{s}\right)&=\frac{\displaystyle\text{V}_\text{o}\left(\text{s}\right)}{\displaystyle\text{V}_\text{i}\left(\text{s}\right)}\\ \\ &=\frac{\displaystyle\left(\frac{\displaystyle1}{\displaystyle\text{sC}_1}+\text{sL}\right)\left(\text{R}_4+\text{R}_5\right)+\text{R}_4\left(\frac{\displaystyle\text{R}}{\displaystyle1+\text{sC}_2\text{R}}+\text{R}_5\right)}{\displaystyle\left(\frac{\displaystyle1}{\displaystyle\text{sC}_1}+\text{sL}\right)\text{R}_4+\text{R}_5\left(\text{R}_1+\frac{\displaystyle1}{\displaystyle\text{sC}_1}+\text{sL}+\text{R}_4\right)} \end{split}\tag6 \end{equation}
Now, when the wiper of the potentiometer is in the middle we set \$\text{R}_4=\text{R}_5:=\text{R}_x\$ and end up with:
$$\mathscr{H}\left(\text{s}\right)=\frac{\displaystyle2\text{C}_1\text{C}_2\text{LR}\text{s}^3+\text{C}_1\left(2\text{L}+\text{C}_2\text{RR}_x\right)\text{s}+\left(2\text{C}_2\text{R}+\text{C}_1\left(\text{R}+\text{R}_x\right)\right)\text{s}+2}{\displaystyle2\text{C}_1\text{C}_2\text{LR}\text{s}^3+\text{C}_1\left(2\text{L}+\text{C}_2\text{R}\left(\text{R}_1+\text{R}_x\right)\right)\text{s}^2+\left(2\text{C}_2\text{R}+\text{C}_1\left(\text{R}_1+\text{R}_x\right)\right)\text{s}+2}\tag7$$
I used Mathematica to solve for the transfer function, the code I used is provided:
In[1]:=Clear["Global`*"];
Vp = Vx;
Vm = Vx;
FullSimplify[
Solve[{I2 == I1 + I3, I1 == (Vi - Vp)/R1, I2 == (V - 0)/R2,
I3 == (Vo - Vm)/R3, I1 == (Vp - V)/R4, I3 == (Vm - V)/R5}, {I1, I2,
I3, Vx, Vo, V}]]
Out[1]={{I1 -> (R5 Vi)/(R2 R4 + (R1 + R2 + R4) R5),
I2 -> ((R4 + R5) Vi)/(R2 R4 + (R1 + R2 + R4) R5),
I3 -> (R4 Vi)/(R2 R4 + (R1 + R2 + R4) R5),
Vx -> ((R4 R5 + R2 (R4 + R5)) Vi)/(R2 R4 + (R1 + R2 + R4) R5),
Vo -> ((R4 (R3 + R5) + R2 (R4 + R5)) Vi)/(
R2 R4 + (R1 + R2 + R4) R5),
V -> (R2 (R4 + R5) Vi)/(R2 R4 + (R1 + R2 + R4) R5)}}
