4

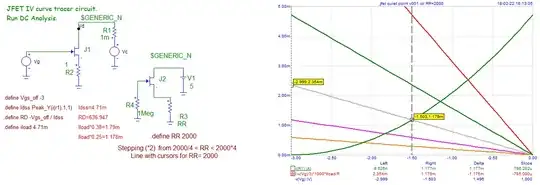
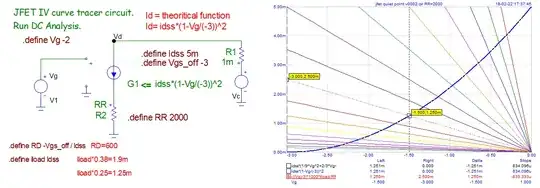
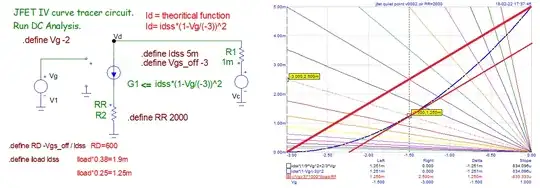
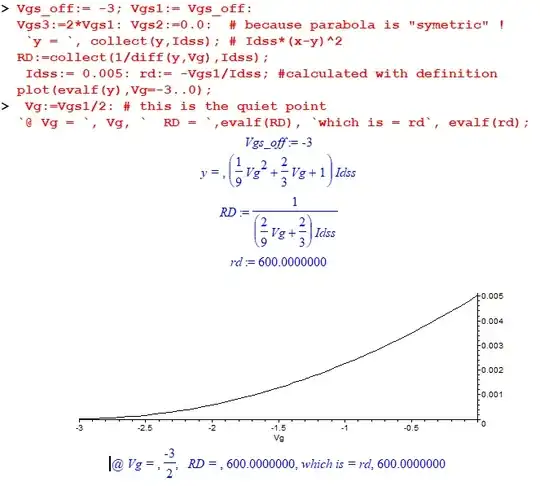
When \$R_s=R_{DS} = \frac{-V_{GS(OFF)}}{I_{DSS}}\$, my textbook seems to suggest that \$I_{D}\$ equals \$\frac{I_{DSS}}{4}\$, but I'm not able to derive this. Any help?

My work:
\$I_D = I_{DSS}(1-\frac{V_{GS}}{V_{GS(OFF)}})^2 \$

\$V_{GS} = -I_DR_s = I_D\frac{V_{GS(OFF)}}{I_{DSS}} \implies \frac{V_{GS}}{V_{GS(OFF)}}= \frac{I_D}{I_{DSS}}\$

Solving these two equations (parabola, straight line) gives me
$$\frac{I_D}{I_{DSS}} = \frac{3 \pm \sqrt{5}}{2} $$

\$\frac{3-\sqrt{5}}{2} \approx 0.38 \ne \frac{1}{4}\$

What does the author mean when he says the drain current will be \$1/4\$ of \$I_{DSS}\$ and \$V_{GS}\$ will be half the cutoff voltage?

From my work, the operating point has equal ratios: \$\color{purple}{(0.38V_{GS(OFF)}, 0.38I_{DSS})}\$

I don't see how the operating can ever be \$\color{red}{(\frac{1}{2}V_{GS(OFF)}, \frac{1}{4}I_{DSS})}\$ as the author claims.

enter image description here

across
  • 1,150
  • 12
  • 26
  • 1
    textbook source: https://archive.org/details/ElectronicPrinciples8thEdition/page/424/mode/2up?view=theater – across Feb 18 '22 at 07:56
  • 2
    They are discussing the ratio of Id to Idss (and I know you know that much already from your writing above) vs the ratio of Vgs to Vgsoff. In short, if $A=\frac{I_D}{I_{DSS}}$ and $B=\frac{V_{GS}}{V_{{GS}_{OFF}}}$ then $A=\left(1-B\right)^2$. No need to solve two equations simultaneously to know that when $B=\frac12$ that $A=\frac14$. Solve them simultaneously if not looking to compare the ratios but instead computing the actual intersection, given some curve. But expect different values for different curves. – jonk Feb 18 '22 at 09:42
  • $B=1/2$ gives $A=1/4$. I'm fine with this. But the author is saying this happens when the source resistor value is $\frac{V_{GS(OFF)}}{I_{DSS}}$ – across Feb 18 '22 at 09:48
  • Which is clearly wrong because, in self bias $V_{GS} = -I_D*R_s$ – across Feb 18 '22 at 09:50
  • When I set $ R_s = \frac{V_{GS(OFF)}}{I_{DSS}} $ , I get $ V_{GS} = -I_D* \frac{V_{GS(OFF)}}{I_{DSS}}$ – across Feb 18 '22 at 09:52
  • But that is same as saying the ratios are equal: $B = A$ – across Feb 18 '22 at 09:54
  • $\dfrac{1}{2} \ne \dfrac{1}{4}$ I'm confused what the author means @jonk – across Feb 18 '22 at 09:55
  • In short: The author says $R_s = \frac{V_{GS(OFF)}}{I_{DSS}}$ gives the operating point $(1/2, 1/4)$. But my work shows the operating point has to be $(0.38, 0.38)$. Who is correct @jonk – across Feb 18 '22 at 09:58
  • 1
    Perhaps you should write a little more in your question, rather than writing it all down in comments. But looking forward in the text I see where you get your equation from the author. I can also see where that term comes from in the simultaneous solution, too. If you solve for Id and then divide that by Idss to get the ratio, you should see there is a factor of (Vgsoff/Idss) in the result. But it is not the only factor. So I am not sure I can explain their claim, just yet. – jonk Feb 18 '22 at 10:04
  • Oh sorry I'll update the question, thank you so much for taking time to understand my question. I notice: setting $R_s=\frac{V_{GS(OFF)}}{I_{DSS}}$ is same as solving the system of equations: $A = (1-B)^2$ and $A=B$ – across Feb 18 '22 at 10:05
  • @jonk updated the question... hope it is clear now thanks again! – across Feb 18 '22 at 10:26
  • 2
    Start with $\frac{I_{\text{D}}}{I{\text{DSS}}}=\left(1-\frac{V{\text{GS}}}{V{{{\text{GS},}\text{OFF}}}}\right)^2$, $V_{\text{GS}}=-R{\text{S}},I{\text{D}}$, and $R{\text{S}}=\frac{-V{{{\text{GS},}\text{OFF}}}}{I_{\text{DSS}}}$ (their claim on the following page.) Then the claim they make is this: $$\frac{I{\text{D}}}{I{\text{DSS}}}=\left(1-\frac{R{\text{S}},I{\text{D}}}{R{\text{S}},I{\text{DSS}}}\right)^2=\left(1-\frac{I{\text{D}}}{I{_\text{DSS}}}\right)^2$$ – jonk Feb 18 '22 at 10:37
  • 1
    But $\frac{I_{\text{D}}}{I{\text{DSS}}}\ne \left(1-\frac{I{\text{D}}}{I{_\text{DSS}}}\right)^2$, even as, for example, a Taylor's approximation around $\frac14$. Not even close. Are we on the same page, here? – jonk Feb 18 '22 at 10:37
  • Yes $x = (1-x)^2$ is not an identity it is true only for two values: $x = \frac{3\pm\sqrt{5}}{2}$ – across Feb 18 '22 at 10:41
  • So where do you want to go from here? I think we agree where their claim leads. – jonk Feb 18 '22 at 10:42
  • I'm just confused is all... you agree the claim by author is incorrect?guess im back to sanity xD @jonk – across Feb 18 '22 at 10:44
  • I don't see how to escape the conflict. The only remaining thing to do is to try and run a set of simulations with a Spice program to verify your conclusion. If Spice shows their claim to be correct, then both you and I are back to the drawing board. If Spice confirms your conclusion, then you have found an error in a textbook. – jonk Feb 18 '22 at 10:46
  • Ok it helps a lot that you confirm I didn't make an error in understanding the textbook. I have LTSpice.. I'll simulate later. But I have more clarity now after discussing with you. Thank you so much you're awesome! – across Feb 18 '22 at 10:52
  • It is frustrating the author uses the same approximation in many example problems https://prnt.sc/zDMzvEVCUIBN – across Feb 18 '22 at 10:53
  • I think you followed it well! But then I'd think that since I agree with you. So my opinion doesn't add anything new and is therefore worthless. ;) – jonk Feb 18 '22 at 10:54
  • @jonk ... I have some explanation after simulating ... In fact, I "found" that RDS (defined as RDS=Vgs_off/Idss) is the value of the "dynamic" resistance at the chosen Quiet Point (???) Q point in ratios (1/2,1/4). – Antonio51 Feb 18 '22 at 19:02
  • 2
    @Antonio51 Thanks! Excellent catch! But I'd love it if you wrote more, including the equation derivations so that it is captured here. :) Makes a LOT of sense. Spice should be able to capture the slope at that point with .MEAS card, I think. – jonk Feb 18 '22 at 19:34
  • 1
    @jonk Done. It was really a good question. I remembered me ~ 50 years ago :-) – Antonio51 Feb 18 '22 at 20:52

1 Answers1

3

Here is a simulation with generic JFET.
At the left, the characteristic (Id vs Vg) is traced.
An after, also load line.
At the right, test with the values found of Idss.

enter image description here

EDIT: NB: Chosen points are not the same as above. (Vgsoff = -3V, Idss = 5mA)
As I was curious about the OP question, I made also a simulation with the theoretical function.
And the result seems that "RDS" is 600 Ohm = 3 V/ 0.005 mA.

enter image description here

But, I have some explanation after simulating ...
In fact, I "found" that RDS (defined as \$RDS = Vgs_off/Idss\$) is :
the value of the "dynamic" resistance at the chosen Quiet Point,
Q point in ratios (\$Vgs = 1/2 * Vgsoff, Id = 1/4 * Idss\$).

Graphical construction:

  1. draw the line through the two characteristic points of the graph (Vgsoff and Idss).
  2. Draw the tangent to the point of contact with the parabola
    at (Vgs = 1/2 * Vgsoff, Id = 1/4 Idss). This tangent is parallel to the other line and is, by definition, the dynamic resistance at the contact point.

enter image description here

This is confirmed by my calculus with Maple sheet.
Calculate the derivative (or measure it on graph) at the quiet point, and the value is exactly RDS.

enter image description here

enter image description here

Antonio51
  • 13,128
  • 1
  • 7
  • 22
  • Nice graphs! I have a question... Is 636.947 ohm value the same as VGSOFF/IDSS ? but from the slope of red-line it seems you're using 1600 ohm resistor at source? Also did you use datasheet to find the value of VGSOFF/IDSS ? – across Feb 18 '22 at 14:47
  • Right. The second graph is ok, I think. I must correct the first, I made a "little" error ("*" replaced by "/") in the function of the load line. (not simple when the graph is on the negative x-axis ...) – Antonio51 Feb 18 '22 at 16:52
  • Wow these are simply awesome! which tool you're using to plot these graphs? matlab? From these graphs it seems when $R_s = 2*R_{DS} = 1200$ ohm, we have the Q point in ratios $(1/2, 1/4)$. that is in actual values $(-1.5, 1.25)$ very enlightening! thank you so much! – across Feb 18 '22 at 17:03
  • 1
    Simulations made with microcap v12 free software http://www.spectrum-soft.com/download/download.shtm – Antonio51 Feb 18 '22 at 17:36

  • Is 636.947-ohm value the same as VGSOFF/IDSS? <<< All values came from the graph, for a generic JFET with some parameters I did not change, just measured on graph by software (function Idss_peak ...).

     – Antonio51 Feb 18 '22 at 17:41
  • @across See my updated answer ... for the "explanation" of RDS. – Antonio51 Feb 18 '22 at 19:17
  • 1
    I feel you've just demonstrated the Mean Value Theorem : instantaneous rate equals average rate at some point. Average rate of current in the interval $(V_{gsoff},0)$ is $\frac{I_{DSS}}{V_{gsoff}}$. Instantaneous rate of current is

    $$\frac{dI_D}{dV_{gs}} = \frac{d}{dV_{gs}} I_{DSS}(1-\frac{V_{gs}}{V_{gsoff}})^2 = I_{DSS}\cdot 2\cdot(1-\frac{V_{gs}}{V_{gsoff}})(\frac{-1}{V_{gsoff}}) = \frac{2I_{DSS}}{V_{gsoff}^2}(V_{gs}-V_{gsoff})$$

     – across Feb 19 '22 at 01:42
  • 1
    When $Vgs=\frac{V_{gsoff}}{2}$, that expression equals $\frac{I_{DSS}}{V_{gsoff}}$ and this is the maximum possible conductance for the jfet in ohmic region! Wow! so the author isn't entirely inaccurate haha Thanks again:) – across Feb 19 '22 at 01:46