0

I am going through The Art of Electronics, 3rd Edition improved. In chapter 12.4.4, Protecting power switches, Figure 12.45 shows current limiting the high side switch; B: fixed current limit:

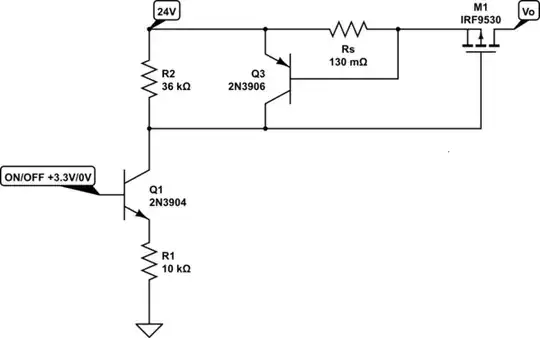
schematic

simulate this circuit – Schematic created using CircuitLab

When Q3 is not conducting (VBE < 0.6V), the Q1 transistor converts the +3.3V logic-level input into a 0.27 mA sinking current (When Q1 is on: I_E at Q1 = ((3.3-0.6)/10k) = 0.27 mA, V_R2 = 36 k * 0.27 mA = 9.72 V), which generates the ~14 V negative-going gate drive for the P-channel M1. So far so good.

How can I now calculate the M1 gate voltage when Q3 is conducting?

The circuit can also be made more precise (V_BE of Q3 uncertainties) for example with replacing Q3 with a differential amplifier. Would it be the solution here:

Current limiter with low voltage drop?

JYelton
  • 34,119
  • 33
  • 145
  • 265
Cahir
  • 61
  • 4
  • When Q3 starts to conduct the gate of M1 is pulled higher (closer to Vcc). The exact gate voltage depends on M1 characterictic. You can approximately read it from datasheet in way how much Vgs is needed to open 4A Id. –  Aug 19 '21 at 03:14

2 Answers2

3

How can I now calculate the M1 gate voltage when Q3 is conducting?

With Rs at 0.13 Ω, the current that flows to start turning Q3 on (and thus start lowering the gate source voltage of M1) is about 5 amps. This is based on 5 amps flowing through Rs producing a base-emitter voltage of 0.65 volts. So, at round about 5 amps, the circuit starts to limit the current.

Next, you open the data sheet for the IRF9530 and see this graph (that I've marked-up in red): -

enter image description here

So, the gate source voltage will be around -4.8 volts and, if the supply is 24 volts then the gate voltage relative to ground is 19.2 volts.

Q3 won't be fully conducting at this point; it'll be partially conducting as per this graph: -

enter image description here

And, if there were a -4.8 volt contour line (I've added one in blue) you'd find that the drain-source voltage would be about 10 volts and the MOSFET would be dissipating about 50 watts.

You then need to ask yourself how long this device will survive current limiting like this. I'll leave you to figure that out from this graph of which I've added some colourful clues (take note of the title of the graph): -

enter image description here

The circuit can also be made more precise (V_BE of Q3 uncertainties)

The big uncertainties are not the BJT but the MOSFET itself and variations in gate-source voltage that produce such and such a drain current.

Would it be the solution here (link in question)?

It's not clear what you are actually comparing that with.

Andy aka
  • 456,226
  • 28
  • 367
  • 807
  • Please don't call out other people (leave the person out of it, discuss only the issue). I've cleared the comments, it would probably be best to end the discussion. – Voltage Spike Aug 18 '21 at 20:29
  • Thanks Andy_aka for your answer. It helped me a lot. – Cahir Aug 18 '21 at 21:38
  • @Andy aka. Sure the uncertainties are in MOSFET but I am interested in taking off the uncertainties in the current limit (Vbe of Q3) over temperature. If I follow the comment from the book, how would the circuit wit a differencial amplifier insted of Q3 look like? – Cahir Aug 18 '21 at 21:50
  • There are no uncertainties in low current BJT's. They have well-defined characteristics and make excellent thermometers. The big tolerances on the Vt of the FETs do NOT create uncertainties in the OCP limit. (in spite of false claims in this answer) The only requirement is that the FET can handle the limit required. Q1 has enough gain to overcome all FET Vt range. But then you will have issues with Over Temp.Protection (OTP) which the thermal characteristics of Vbe thermally connected to the FET will help reduce the current limit. Basically you need OCP and OTP so your specs are incomplete. – Tony Stewart EE75 Aug 19 '21 at 02:45
-1

enter image description here

How can I now calculate the M1 gate voltage when Q3 is conducting?

That’s not important as long as RdsOn can limit the current over the gate voltage range more than Vt.

Here with M1 that has a suitable low RdsOn to allow current limiting, the current limit will always be exactly Imax= Q3-Vbe/Rs. The Vgs will be just enough above Vt threshold for any load that draws this current.

Since the input controls the Q3 current as M1 draws no gate current in the static condition, and Q1,Q3 BJT’s are in high impedance current sinks, Vbe will change very slightly with Ic-Q3 and thus Vbe/Rs=Io.

This configuration is independent of hFE and gm of the M1 as long as the Vgs exceeds Vt by a sufficient amount to draw Io.

Vt will affect the Vgs voltage with the square-law controlled Ron resistance but in this closed loop the current will always be dominated by Q3 Vbe to limit the Io Current as the gate draws almost no current.

Ambient temperature of course will have the NTC effects on Io from Vbe.

If IcQ1=0.27mA, IcQ3 will be much less and Vbe will be between 0.5 and 0.6 V which can be computed.

Thus Io(max)= 550 mV/130m = 4.2 A within 10%. due to my estimate of Q3-Vbe.

Proof

To prove my assertions,

  1. Imax tracks Rs exactly.
  2. Imax is independent of hFE for the PNP.

To prove both, I used hFE=1 by reversing the PNP transistor and plotted Vcb with an ammeter shown. M1 has a sufficiently low RdsOn and Vt to draw the sensed current and cannot exceed the current limit of Rs.

The load is controlled by a pot on a Darlington. I_out= Vcb just as it would for Vbe if the PNP were not reversed, however the Veb would be exceeding it’s rating of -5V for 24V supply. But this proves the diode current mirror effect of the Rs exactly limits the current with high loop gain from gm of Q1 * M1 .

Tony Stewart EE75
  • 1
  • 3
  • 54
  • 185