Why do they place the graph of the input voltage in such a slanted way?
I do not get it.
Is there a Pythagorean relationship?
What is the reason for that provision, is a question that I have had for several days.
I have found another image with the same arrangement, but now instead of the input voltage, the sloped base current appears.
That confuses me, I don't know which one is correct
For starters, here's a discussion of the AC load line for a BJT amplifier: BJT: What exactly is an AC Load line?
The slanted sine wave shows the excursions of the point \$(i_c, v_{ce})\$.
This point is constrained to the AC load line.
As the collector current \$i_c\$ oscillates about the Q-point current, the point \$(i_c, v_{ce})\$ will oscillate along the AC load line about the Q point, and that's why they draw its time-evolution graph in a slanted manner. They are just showing how far up and down that AC load line that point moves. It's natural to show the time-evolution of this point in a direction that is perpendicular to the load line.
The same can be said when \$v_{ce}\$ oscillates about the Q-point voltage.
Note that \$i_c = \beta_{ac}i_b\$, so saying that \$i_c\$ oscillates is the same as saying that \$i_b\$ oscillates.
The same can be said for (AC) input voltage and \$i_b\$.
This assumes an emitter resistor to linearize Vb and Ib, so the load line for each is linear in theory. In practice the load line slope rises at. Vce(sat)and gain reduces rapidly.
Otherwise it is just showing how the slope of Rc is linear when Re >>re ? Also when Ic reduces with re=26/Ic , re rises and may approach Re if small <100 and thus the slope changes and 2nd order distortion may occur ( maybe Vce<2V when Re is not <<Re)
Plotting characteristics curves with load lines is sui generis an exercise in computational geometry, and, as we see from the OP's question, only few professors (textbooks, course notes) elucidate the subject comprehensively.
Both figures in the question lack the most important constituent, output characteristic curves. I have no readily available pictures at hand to illustrate my answer with graphs of BJT output characteristic curves with the load line, but we can discuss slide 28 from EE3950 Class Notes Chapter 11, Louisiana State University with output characteristic curves for common source amplifier.
The slide shows all the necessary visuals: output characteristic curves, the load line, the input ac voltage (slanted!) and the output voltage -- here it is \$v_{DS}\$, but with \$v_{CE}\$ you have a similar picture.
The most prominent feature of the load line is that the metric for measuring distances along this line is neither volts of the horizontal axis \$V_{DS}\$ (the OP's \$V_{CE}\$) nor milliamperes of the vertical axis \$I_D\$ (the OP's \$I_C\$). Each point of the load line is mapped to a voltage, but this voltage is not the projection of the load line point to the horizontal axis: by definition it is the voltage of the characteristic curve \$V_{GS}\$ (the OP's \$I_b\$) which intersects the load line at this point. Therefore, you cannot use the Euclidean distance (apply the Pythagorean theorem) when computing the input voltage \$v_{GS}\$ (the OP's input current \$i_b\$) for a given output voltage \$v_{DS}\$ (the OP's \$v_{CE}\$). You look for the voltage of the characteristic curve that intersects the load line at the same point where the tangent of the envelope's maximum intersects the load line (the 4V dashed line in slide 28): it is the maximum of the input signal waveform voltage. Then you look for the voltage of the characteristic curve that intersects the load line at the same point where the tangent of the envelope's minimum intersects the load line (the 2V dashed line in slide 28): it is the minimum of the input signal waveform voltage.
The Pythagorean theorem does not help you find maximum/minimum of input signal voltages given output signal waveform. The projective geometry is your tool for computations based on intersections of the load line and characteristic curves!
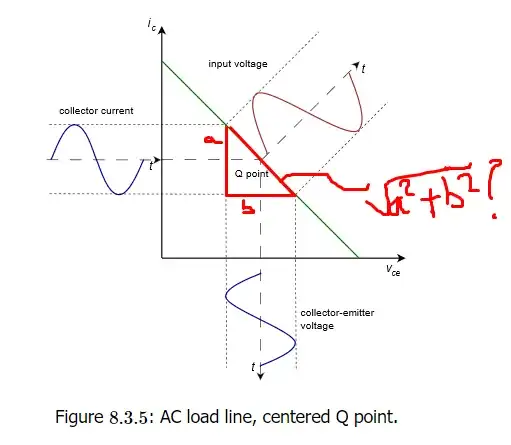
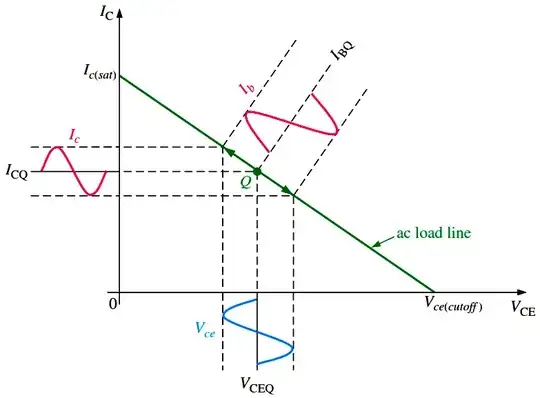
BJT Small Signal Analysis
Image below taken from page 4 of this reference:
http://www.iitg.ac.in/apvajpeyi/ph218/Lec-8.pdf
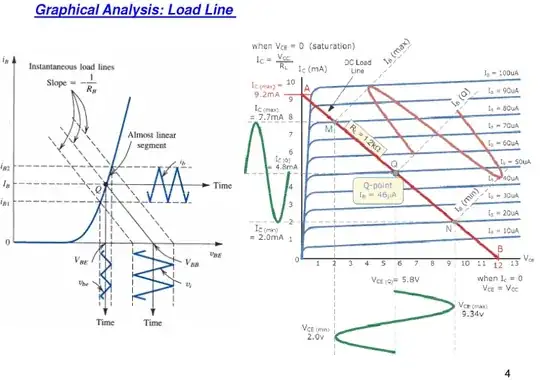
Input Dynamic Load Line Analysis
The input load line analysis is shown on the left side graph. The DC Q point is set by the bias design and the AC variation depends on the magnitude of the AC input signal.
Output Dynamic Q-Point Load Line Analysis
The output load line analysis is shown on the right side graph. The Q-point is constrained to a location on the output load line. The axis shown represent the value for these variables of interest:
$$I_C, V_{CE},I_B$$
with the assumption that the AC small signal input waveform is a sinusoidal waveform.
Note the vertical axis refers to the collector current in units of ampere. The horizontal axis refers to the collector-emitter voltage in volts. The product of current and voltage is power given in watts. One can draw an operating point vector with the tail at zero (origin) and the head at the Q-point. Then the collector current is the projection of this vector onto the vertical axis and the collector-emitter voltage is the projection of this vector onto the horizontal axis. The area under the dynamic Q-point, based on these projections, is the power dissipation in the output side of the transistor at a point in time. The maximum voltage, current, and power ratings for the transistor would be given by a safe operating area (not shown in the curves above).
Note the diagonal base current axis and the characteristic curves for constant base current are overlays placed "on top of" the horizontal and vertical axes used for output load line analysis. If drawn to scale the collector current would be the forward current gain times the value indicated as constant base current in the characteristic curves. The proper way to interpret either a voltage or current axis along the load line is that is it is a separate graph of physical properties superimposed on the output graph at an angle so its vertical axis corresponds to the load line.
