BJT: What exactly is an AC Load line?

Question

The DC Load Line is simple to explain, for a given circuit the relation between V_CE and I_C must comply to the KVL relationship for that circuit.

In the graph we can choose a Q point, and then see if we superimpose an AC signal on top of the DC voltage then the V_C will follow accordingly, and we can determine the maximum output swing.

The AC Load Line confuses me however. Because when I determine this line using the AC equivalent circuit model and KVL across the v_ce loop, the load line now goes through zero on a graph.

i_c = - v_ce / (R_C // R_L)

Then I understand to get the true load line of the circuit, I must superimpose the AC Load line on the Q point, and preferably use the middle of the AC LL as the Q point.

I then get this:

• Does this mean the DC LL no longer stands?
• How did we get the I_max and V_max of the AC LL?
• And how do I determine the Q point to be in the middle of the AC LL?

Thanks

Answer 1

(This is a rather longish answer to dig a little deeper into the connection between the AC load line and the maximum collector current and collector-emitter voltage).

What exactly is an AC Load line?

In words, and for this circuit, it is the plot of the collector current versus the collector-emitter voltage with the emitter bypass and collector coupling capacitors replaced with batteries with each battery voltage equal to the respective quiescent capacitor voltage.

^{simulate this circuit – Schematic created using CircuitLab}

We'll get to why later. First, let's verify that this will give the AC load line.

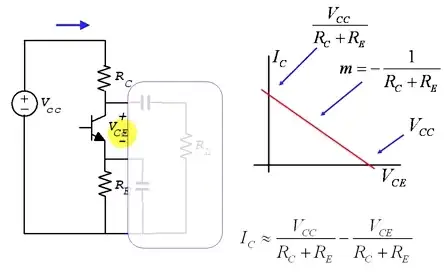
When the collector current is zero, the collector voltage is, by voltage division

$$V_{C,max} = (V_{CC} - V_{CQ})\frac{R_L}{R_C + R_L} + V_{CQ} = I_{CQ}R_C||R_L + V_{CQ}$$

Thus,

$$V_{CE,max} = V_{C,max} - V_{EQ} = I_{CQ}R_C||R_L + V_{CEQ}$$

Assuming, for simplicity, that the saturation voltage is zero, \$V_{CE,sat} = 0V\$, the maximum collector current is

$$I_{C,max} = \frac{V_{CC} - V_{EQ}}{R_C} + \frac{V_{CQ} - V_{EQ}}{R_L} = I_{CQ} + \frac{V_{CEQ}}{R_C||R_L}$$

So, we have two located two points on the graph of \$i_C\$ versus \$v_{CE}\$

$$i_C = 0, v_{CE} = I_{CQ}R_C||R_L + V_{CEQ}$$

$$i_C = I_{CQ} + \frac{V_{CEQ}}{R_C||R_L}, v_{CE} = 0$$

The equation for the line through these two points is a load line and given by

$$i_C = I_{CQ} + \frac{V_{CEQ}}{R_C||R_L} - \frac{v_{CE}}{R_C||R_L}$$

Now, this load line has two notable characteristics:

(1) for \$v_{CE} = V_{CEQ}\$, the collector current is \$i_C = I_{CQ}\$ so this load line is through the quiescent point.

(2) the change in collector-emitter voltage is \$\Delta v_{CE} = -\Delta i_C R_C||R_L\$

But this is just the AC load line!

---

Returning to the question of why replace the capacitors with batteries. Recall that, for AC analysis, the bypass and coupling capacitors are considered AC short circuits, i.e., the AC voltages across the capacitors are zero.

Thus, from a total (DC + AC) voltage perspective, the total voltages across the capacitors are constants and equal to their quiescent voltages.

In other words, if we assume the capacitors are AC short circuits for signal analysis, we can replace the capacitors with constant voltage sources, i.e., batteries for this DC + AC analysis.

Answer 2

Load lines shows the behavior linear components in the circuit. DC load line gives the I-V relationship in the DC equivalent circuit. The inverse of slope of DC line gives the DC load resistance, \$R_E+R_C\$.

AC load lines give the I-V relationship when AC equivalent model is considered. But the AC load seen by the amplifier, \$r_c=R_C||R_L\$, is different from the DC load and hence the slope of AC load line is different. But these two lines intersect at the point where AC signal part becomes \$0\$. ie, at Q point.

• DC load line is applicable only when DC equivalent circuit is considered.

• After calculating Q point (\$I_{CQ},V_{CEQ}\$) from DC load line, \$I_{max}\$ and \$V_{max}\$ can be calculated as, $$I_{max} = I_{CQ} + \frac{V_{CEQ}}{r_c}$$ $$V_{max} = V_{CEQ} + I_{CQ}r_c$$

• Putting Q-point in middle means: \$I_{max} = 2I_{CQ}\$ and \$V_{max} = 2V_{CEQ}\$. Comparing this equations with equations for \$I_{max}\$ and \$V_{max}\$, it is clear that the value of \$r_c\$ should be \$V_{CEQ}/I_{CQ}\$. So after drawing DC LL, select Q-point such that $$\frac{V_{CEQ}}{I_{CQ}} = r_c$$ This will fix the Q point in the middle of the AC LL.