The two OR gates you see are negative logic, which has the same truth table as NAND. DeMorgan's Theorem tells us so.
That is,
- Negative-logic (Demorgan) OR: Y = !A + !B
is the same as:
- positive-logic NAND: Y = !(A & B)
Work out the truth table for each, you will see that they are the same.
What the authors intent seems to be is to convey is that if you have choices for the signal polarity (notice in the second diagram they use B' and C', that is, negative-true inverted versions of them) then you can use Demorgan's Theorem to simplify your logic somewhat - if 'simplify' means use all NAND.
As to why they chose to represent the two OR gates as neg-logic OR instead of pos-logic NAND, they seem to want to show similarity in structure to the original logic. That is, those neg-logic ORs occupy the same functional space as the pos-logic ORs in the original diagram.
In the bigger picture, they're encouraging you to think about negative-logic and positive-logic representations of the same gate.
By the way, the same DeMorgan conversion can be done using NOR (neg-logic AND), as was famously done to build the Apollo Guidance Computer. That said, for CMOS there is area and leakage advantages that favor using NAND over NOR. More here: Why is NAND gate preferred over NOR gate in industry?
However, real-world logic used in ASICs and other ICs won't use just one gate type, be it NAND or NOR. Instead, they will use a variety of structures provided by the standard cell library, including efficient and-or-invert (AOI) / or-and-invert (OAI), transmission gate types, as well as custom cells for critical and complex paths like RAMs, ALUs or multipliers. More here: What is the lowest level of CPU programming above transistors?
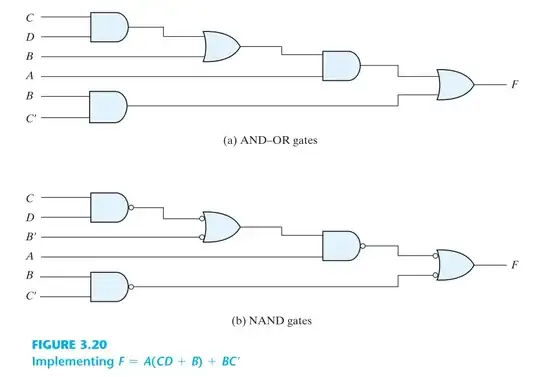
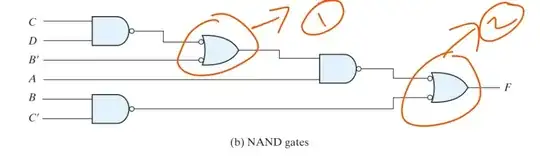
Bof the first circuit changed intoB'of the second circuit. First I thought this is an error... until I saw that little tiny tick. I would have inserted a NAND as inverter. -- Lesson to learn: Things done by humans tend to be inexplicable. ;-) – the busybee Sep 29 '20 at 15:03