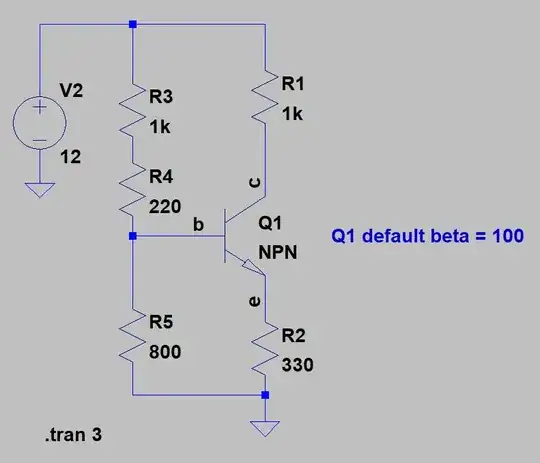
Assuming Active Mode
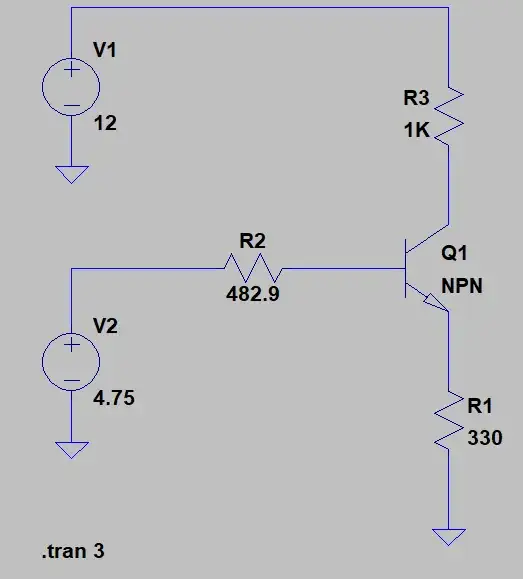
The Thevenin equivalent of your base divider is:
$$\begin{align*}V_{\text{TH}}&=V_\text{CC}\cdot \frac{R_5}{R_3+R_4+R_5}\approx 4.7525\:\text{V}\\\\R_{\text{TH}}&=R_5\cdot\frac{R_3+R_4}{R_3+R_4+R_5}\approx 483.17\:\Omega\end{align*}$$
If you assume that the BJT is in active mode (not saturated) then you come up with the approximate value for the base current this way:
$$\begin{align*}I_\text{B}&=\frac{V_{\text{TH}}-V_\text{BE}}{R_{\text{TH}}+\left(\beta+1\right)\cdot R_2}\approx 120\:\mu\text{A}\end{align*}$$
From this, you and work out that the expected voltage drop across the collector resistor would be in excess of \$\beta\cdot R_3\cdot 120\:\mu\text{A}\approx 12 \:\text{V}\$. This, alone, tells you that the circuit is saturated.
So the assumption for active mode is wrong.
Saturated Mode Conclusion
The new circuit, now that you know it is saturated, looks more like this. Using \$V_\text{SAT}=100\:\text{mV}\$ and \$V_\text{BE}=700\:\text{mV}\$, for example, it's:
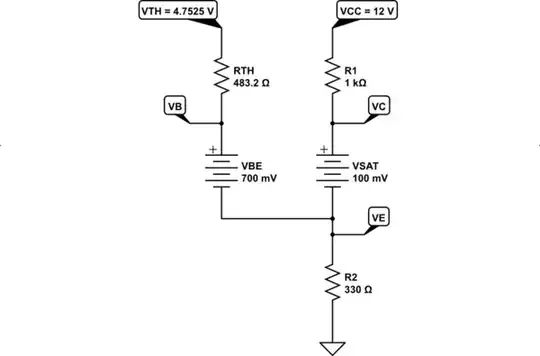
simulate this circuit – Schematic created using CircuitLab
(Note that in saturated mode, the collector looks more like a voltage source and not like a current source [as it does when in active mode.])
At this point, use nodal analysis to solve:
$$\begin{align*}
\frac{V_\text{B}}{R_\text{TH}}+I_{V_\text{BE}}&=\frac{V_\text{TH}}{R_\text{TH}}\\\\
\frac{V_\text{C}}{R_1}+I_{V_\text{SAT}}&=\frac{V_\text{CC}}{R_1}\\\\
\frac{V_\text{E}}{R_2}&=I_{V_\text{BE}}+I_{V_\text{SAT}}\\\\
V_\text{B}&=V_\text{E}+V_\text{BE}\\\\
V_\text{C}&=V_\text{E}+V_\text{SAT}\\\\
&\therefore\\\\
V_\text{E}&\approx 3.326\:\text{V}\\\\
V_\text{B}&\approx 4.026\:\text{V}\\\\
V_\text{C}&\approx 3.426\:\text{V}\\\\
\mid\, I_\text{B}\mid=I_{V_\text{BE}}&\approx 1.504\:\text{mA}\\\\
\mid\, I_\text{C}\mid=I_{V_\text{SAT}}&\approx 8.574\:\text{mA}\\\\
\mid\, I_\text{E}\mid=I_{R_2}= \frac{V_\text{E}}{R_2}&\approx 10.078\:\text{mA}
\end{align*}$$
That's the complete analysis for the circuit.
Summary
For small signal BJTs, \$V_\text{BE}=700\:\text{mV}\$ when \$I_\text{C}\approx 1.5-2.0\:\text{mA}\$. Clearly, this collector current is more than that range. So I'd expect about \$26\:\text{mV}\cdot\operatorname{ln}\left(\frac{8.574\:\text{mA}}{1.5\:\text{mA}}\right)\approx 45\:\text{mV}\$ higher, or \$V_\text{BE}\approx 745\:\text{mV}\$. You could go back through the process and come up with a refined quantitative calculation. But the above analysis is already close enough and BJTs vary, anyway. So there's no real need to do more.
(Also note that you are using a default BJT in Spice and I'm using more practical estimates for typical small-signal BJTs.)