Apparent contradiction on ideal OpAmp equations

Question

For an ideal OpAmp the voltages at the inputs are said to be of equal value and the currents 0, however, for we also know that $$V_\text{out}=A(V_p-V_n)$$ but if the voltages are the same the output should always be 0!

I know that what I'm saying is wrong, but I don't know where the loophole is, and I can't find it anywhere.

An important consideration for a correctly configured negative feedback amplifier is that both $\small I_p$ and $\small I_n$ are zero (or close enough to zero to make this assumption valid). And also, negative feedback forces Vn to be almost equal to Vp. The op-amp achieves these characteristics by virtue of its enormous open loop gain and high input impedance. — Chu, Jan 10 '19 at 00:20

score 5 · Accepted Answer · edited Jun 11 '20 at 15:10

For an ideal op-amp the voltages at the inputs are said to be of equal value ...

No. If negative feedback is applied and the output is not driven into saturation then the inputs will be very, very close to equal.

... and the currents 0, ...

Yes, due to the high and sometimes very, very high input impedance.

... however, for we also know that \$ V_{out}=A(V_p−V_n) \$ but if the voltages are the same the output should always be 0!

Correct. And that is why the voltages are not the same (but very, very close). The difference in voltages can be worked out by rearranging your formula to $$ V_p - V_n = \frac {V_{out}}{A} $$ and since A is very large the difference in inputs is very small - so small that it's almost zero.

schematic

^{simulate this circuit – Schematic created using CircuitLab}

Figure 1. Non-inverting amplifier with a gain of 2.

From the comments:

When analyzing an op-amp circuit with negative feedback assuming it is ideal we make the assumptions (almost in this order):

Input voltages are the same;

Yes, but we know deep down that they are slightly different.

The gain of the op-amp goes to infinity;

The gain of the op-amp is fixed as specified in the datasheet. 1M to 10M would be typical.

Work out the output voltage and find out that the gain is finite and dependent of the circuit around the op-amp.

The gain of the complete circuit is "finite" (a modest value, say, of 1 to 1k) rather than the open-loop gain of 1M to 10M which hasn't changed, no matter what the feedback arrangement is.

If in a circuit the only thing that causes a gain is the op-amp then the gain of the circuit is the gain of the op-amp, so our reasoning appears to be flawed.

Nope. You're forgetting the negative feedback. This controls the overall circuit gain and corrects any variations and non-linearities in the op-amp itself.

I think I just got it, my problem now lies in "How" does the negative feedback controls the circuit gain, ...

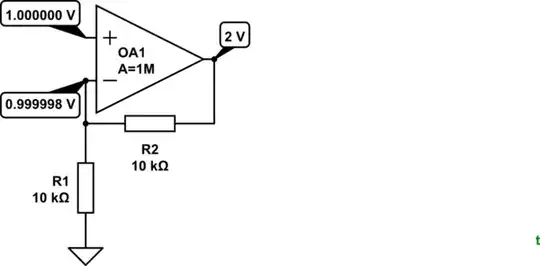
Let's look at Figure 1 again.

Initially V_p is at 0 V so the output and V_n are at 0 V too.
V_P is suddenly and instantly switched from 0 to +1 V.
V_P - V_n = 1 V so (since the open-loop gain of the op-amp itself is 1M) the output starts to swing towards +1,000,000 V at a rate limited by the slew rate of the op-amp.
As it does, V_P - V_n is decreasing and by the time V_out reaches 0.5 V, V_P - V_n = 0.75 V so the output is now trying to swing to 750,000 V (but is still only at 0.5 V). Remember that the feedback is dividing by 2.
This process continues so that as the output gets approaches 2.0 V the difference between the inputs is getting close to zero and so the target output voltage is falling too. The feedback is reducing the output drive and bringing it under control.
Very quickly the output reaches 2.0 V and at this point V_n is just a millionth or two below 1 V and the circuit is stable, balanced, happy and under control.

Thank you for the answer, and that makes sense, but when analyzing an OpAmp circuit with negative feedback assuming it is ideal we make the assumptions (almost in this order):1)Input voltages are the same; 2) The gain of the OpAmp goes to infinity;3) work out the outpout voltage and find out that the gain is finite and dependent of the circuit around the OpAmp. If in a circuit the only thing that causes a gain is the OpAmp then the gain of the circuit is the gain of the OpAmp, so our reasoning appears to be flawed — Bidon, Jan 09 '19 at 22:23
I'm having a hard time distinguishing circuit gain from OpAmp gain, how is it different? — Bidon, Jan 09 '19 at 22:24
Thank you, I think I just got it, my problem now lies in "How" does the negative feedback controls the circuit gain, but maybe I'll google it. If you have the patience to answer I appreciate it but it's okay — Bidon, Jan 09 '19 at 22:49

user2233709 · Answer 2 · 2019-01-09T22:23:45.210

2

The loophole is that, for an ideal op-amp, \$A = +\infty\$. Hence, unless you reach saturation, \$V_p - V_n = {V_{out} \over A} = {V_{out} \over +\infty} = 0\$.

Edit:

If that helps you, you can consider a non-ideal op-amp with a finite \$A\$ gain, using it in an inverter configuration, as you suggested in your comment:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

Then you have both \$V_{out} = A (V_+ - V_-) = A (0 - V_-) = - A V_-\$ and \$V_- = {V_{in} + V_{out} \over 2}\$. That leads to \$V_{out} = - {A \over A+2} V_{in}\$ and \$V_- = {1 \over A+2} V_{in}\$.

Now, when \$A \to +\infty\$, you have \$V_{out} \to -V_{in}\$ and \$V_- \to 0\$.

edited Jan 09 '19 at 22:23

answered Jan 09 '19 at 22:01

user2233709

1,735
9
15

But if you do the calculations using the equality $V_p=V_n$, say for the inverter configuration, you get a gain that is finite, thus it contradicts our initial proposition ($A \to \infty $) – Bidon Jan 09 '19 at 22:04
@Bidon $A$ is the gain of the op-amp, not the gain of the whole circuit built around the op-amp. – user2233709 Jan 09 '19 at 22:08
But even so, again in an inverter set up for example, the only thing that produces a gain is the OpAmp, so isn't the gain of the circuit the gain of the OpAmp? – Bidon Jan 09 '19 at 22:12
@Bidon I just edited my answer. Hope this helps. – user2233709 Jan 09 '19 at 22:25
It kind of helps, but (I'm really sorry) I don't understand the difference between the gain of the circuit and the gain of the OpAmp. – Bidon Jan 09 '19 at 22:31
1

The input of the op-amp is $V_+-V_-$, its output is $V_{out}$, so its gain is ${V_{out} \over V_+ - V_-} = A$. The input of the inverter circuit is $V_{in}$, its output is $V_{out}$, so its gain is $G = {V_{out} \over V_{in}} = - {A \over A+2} \to -1$. – user2233709 Jan 09 '19 at 22:36
+1. The OP asked about ideal op-amps and you described it perfectly. – Shamtam Jan 09 '19 at 22:43

score 2 · Answer 3 · answered Jan 09 '19 at 22:16

The assumption that the input voltages are always the same only applies when the op amp is used with negative feedback. It is the feedback that causes the input voltages to be the same (or nearly so, in the real world). Of course, we also assume that the output voltage is within the operating limits of the amplifier.

When operated without feedback, or with positive feedback, then the input voltages may be much different. In this case it is reasonable to say that $$V_{OUT} = A_{OL}(V_P - V_N)$$ where \$A_{OL}\$ is the open loop gain of the op amp itself.

analogsystemsrf · Answer 4 · 2019-01-10T04:17:42.877

One formula often used in thinking about opamp behavior is

Closed Loop Gain = G /(1 + G * H)

where G = the open-loop-gain and H is the feedback-factor.

Suppose the G rolls off with frequency, and suppose the H is 0.0001 (purpose is to produce a precision gain of 10,000x). What happens in a real opamp?

Look at the right side axis, where linear-error is plotted, Notice the error is 10%, at 10 Hz.

And 1% error at 1Hz.

And 0.1% error, or 10 bits, at 0.1 Hz.

Apparent contradiction on ideal OpAmp equations

4 Answers4

Linked

Related