I have got the following Schmitt trigger circuit implemented already on a breadboard. As seen, the input signal at the non-inverting and inverting terminals of the op amp is the same, but with the addition of a RC circuit in the inverting terminal. In this way, I am comparing the input signal with a delayed version of the same signal such that I can identify peaks. I got the idea from here.
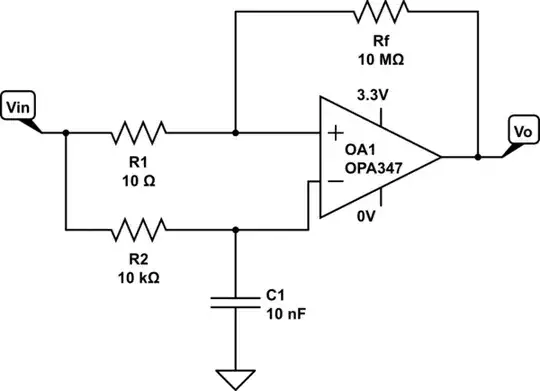
simulate this circuit – Schematic created using CircuitLab
I wanted to obtain its transfer function so as to analyse more carefully the influence of the RC network (and ultimately, the circuit itself). I obtained an expression for \$H(w)\$, created some code in Matlab to plot the transfer characteristic (magnitude and phase) of the circuit, and also implemented the circuit in TI-Tina simulator. Using the Tina's AC analysis, I also plotted the transfer characteristic... and my Matlab results differ from Ti-Tina's results.
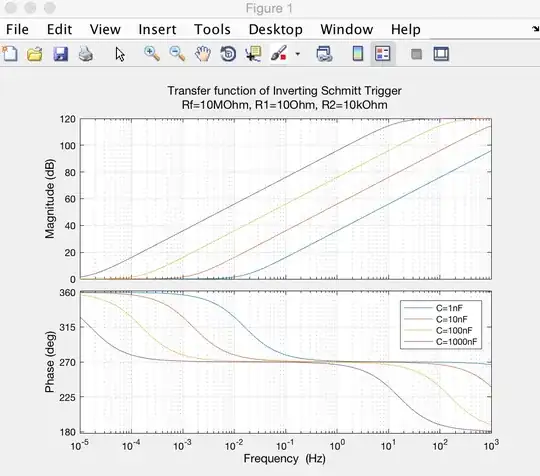
Here the results from Matlab:
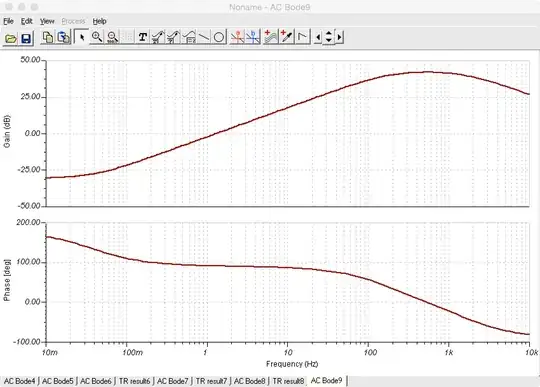
And here the results from TI-Tina:
For this reason I wanted to ask whether the following set of equations to obtain \$H(w)\$ is correct.
The voltage \$V_{+}\$ is:
\begin{equation}
V_{+} = V_{in}\dfrac{R_{f}}{R_{1} + R_{f}} + V_{o}\dfrac{R_{1}}{R_{1} + R_{f}}
\end{equation}
Considering admittances, \$V_{-}\$ is \$V_{-} = V_{in}\dfrac{G_{2}}{G_{2} + sC_{1}}\$. Putting \$s = jw\$ and \$R_{2} = 1/G_{2}\$, we have:
\begin{equation} V_{-} = V_{in}\dfrac{1}{1 + jwC_{1}R_{2}} \end{equation}
As \$V_{+}=V_{-}\$, the following expression can be obtained:
\begin{equation} V_{o} = V_{in}\dfrac{1-jwC_{1}R_{2}R_{f}/R_{1}}{1 + jwC_{1}R_{2}} \end{equation}
Therefore,
\begin{equation} H(w) = \dfrac{V_{o}}{V_{in}}=\dfrac{1-jwC_{1}R_{2}R_{f}/R_{1}}{1 + jwC_{1}R_{2}} \end{equation}
Any insights? I would appreciate your help. Many thanks.
If useful, the code I've used in Matlab is:
%--- We fix Rf and R2 and vary C1
R1 = 10;
Rf = 10e6;
R2 = 10e3;
C1 = [1 10 100 1000] .* 1e-9;
opts = bodeoptions;
opts.Title.String = '';
opts.Title.FontSize = 12;
opts.Xlabel.FontSize = 12;
opts.Ylabel.FontSize = 12;
opts.TickLabel.FontSize = 10;
opts.FreqUnits = 'Hz';
opts.Grid = 'on';
H = [];
for i=1:length(C1)
H = [H tf([-C1(i) * R2 * Rf / R1,1],[C1(i)*R2,1])];
end
figure
hold on
for i=1:length(C1)
bodeplot(H(i),opts);
end
legend_t = cell(length(C1), 1);
for i=1:length(C1)
legend_t{i} = sprintf('C=%snF', num2str(C1(i) * 1e9));
end
legend(legend_t);
title({'Transfer function of Inverting Schmitt Trigger', ...
sprintf('Rf=%dMOhm, R1=%dOhm, R2=%dkOhm', Rf/1e6, R1, R2/1e3)});