Using the equation Ic=Is*e^(Vbe/Vt) yields impossible values for me. I am using Vbe = .7v & Vt = .025 A. Is in circuit is 3.4mA. I am trying to determine Ic as an initial value for analyzing the rest of the circuit, as the rest of the values are unknown. I assume I am missing a convention associated with the magnitude of Vt or Vbe. Is this the case?
Example circuit:
simulate this circuit – Schematic created using CircuitLab
You cannot solve this by assuming the base current is a certain value. Start with \$I_C = \beta I_B\$ and \$V_{BE} = 0.7V\$.
Also, \$I_S\$ is not a circuit current, it is a parameter of the BJT.
You have stated Is = 3.4mA. I notice that if the transistor is saturated, then 24v is dropped across R1+R2, and the current is 3.4mA.
Although Is is called the 'saturation current', it does not mean 'the current that flows in a circuit when the transistor is saturated'. It is a property of the transistor, and usually has a value down in the pA or fA. It's the current drawn by a diode junction when it's reverse biassed.
Attempting to use the wrong value of Is for the wrong purpose will not help you understand a transistor circuit.
In the absence of any other data (you have told us everything that's relevant, haven't you?), you have to make some judicious assumptions, and in this order.
There is an emitter resistor R2. So the application is likely to be a linear circuit, not a saturating switch, which would have the emitter tied directly to ground.
So as it's a linear circuit, you'd expect the collector voltage to be 'sensible', biassed to about half the available voltage swing. If we ignore the base current (a reasonable assumption), then the R1 voltage drop will be 2.5x the R2 drop. Arrange for 12v across these two resistors, and 12v across the transistor. That's about 3v on R2, for a current of 1.5mA. That current will drop about 7.5v across R1.
As there's 3v on the emitter, you'll want 3.7v on the base. Any voltage close to this will result in a 'reasonable' bias point.
I think it is really fantastic that Neil managed to read you correctly. I know I struggled with your wording. But Neil's quick mind and writing makes yours much clearer to me. I wish you'd written your question as well as Neil managed to read it.
The BJT physics is pretty interesting. If you want to understand one of the better models for it, look up the MEXTRAM model. That will give you some reading for a few nights, at least.
The simplest full DC model is the Ebers-Moll model. (There are several versions.) But as you almost write in your question, much of all that model can be reduced to this:
$$I_C=I_{SAT}\left(e^\frac{V_{BE}}{n\: V_T}-1\right)\tag{1}$$
In (1) above, \$I_{SAT}\$ and \$n\$ are model parameters.
The thermal voltage is,
$$V_T=\frac{k\:T}{q}\tag{2}$$
and is based upon 1st principle physics and the equi-partition of energy law.
\$I_{SAT}\$ is the y-intercept in this curve:
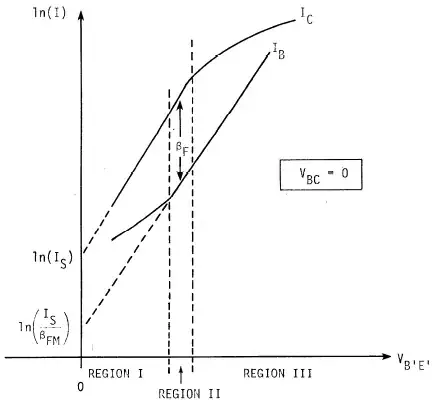
That chart above should help a lot in understanding how this model parameter is arrived at.
\$I_{SAT}\$ is really \$I_{SAT}\left(T\right)\$ and is a very strong function of temperature. So strong, in fact, that it completely overwhelms equation (2) above and reverses the overall sign of the change of \$V_{BE}\$ with respect to temperature!!
Here's an example of the dependence of \$I_S\$ on temperature:
$$I_{SAT}\left(T\right)=I_{SAT}\left(T_{nom}\right)\cdot\left(\frac{T}{T_{nom}}\right)^{3}\cdot e^{\left[\frac{E_g}{k}\cdot\frac{T-T_{nom}}{T\cdot T_{nom}}\right]}\tag{3}$$
Note that \$E_g\$ is the effective energy gap (in eV) and \$k\$ is Boltzmann's constant (in appropriate units.) \$T_{nom}\$ is the temperature at which the equation was calibrated, of course, and \$I_{SAT}\left(T_{nom}\right)\$ is the extrapolated saturation current at that calibration temperature.
The power of 3 used in the equation above is actually a problem, because of the temperature dependence of diffusivity, \$\frac{k T}{q} \mu_T\$. And even that, itself, ignores the bandgap narrowing caused by heavy doping. In practice, the power of 3 is itself often turned into yet another model parameter in Ebers-Moll.
But keep in mind MEXTRAM, too. The Ebers-Moll model went through at least three major revisions before Gummel-Poon arrived. Then the GP model itself went through modifications. Then VBIC became a newer model. Today, it is MEXTRAM in some 5th or 6th major revision by now.
For some more information on Ebers-Moll, see:
Let's modify your circuit, slightly:
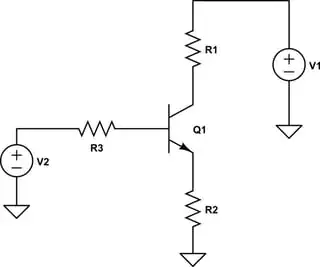
simulate this circuit – Schematic created using CircuitLab
The whole point of arranging the voltage source polarities as shown is that the BJT is either in active mode, or saturated. It's not possible to tell without putting values in, of course.
However, you can still apply KVL:
$$V_2-I_B\cdot R_3 - V_{BE} - I_E\cdot R_2=0\:\text{V}\tag{4}$$
If the BJT isn't saturated (an assumption you may want to start with, since as Neil points out the circuit doesn't look like an intended switch but instead as an analog circuit), then you also know that over a very wide range of operation:
$$\begin{align*} I_E&=\left(\beta+1\right)\cdot I_B\tag{5}\\ I_C&=\beta\cdot I_B\tag{6} \end{align*}$$
Equation (5) inserted into (4) yields:
$$V_2-I_B\cdot R_3 - V_{BE} - \left(\beta+1\right)\cdot I_B\cdot R_2=0\:\text{V}\tag{7}$$
From that, we find:
$$I_C=\beta\cdot\frac{V_2-V_{BE}}{R_3+\left(\beta+1\right)\cdot R_2}\tag{8}$$
But now we can insert equation (1) into (8):
$$I_{SAT}\left(e^\frac{V_{BE}}{n\: V_T}-1\right)=\beta\cdot\frac{V_2-V_{BE}}{R_3+\left(\beta+1\right)\cdot R_2}\tag{9}$$
Which you can use to solve for \$V_{BE}\$:
$$\begin{align*} \text{Set: } V_Z &= I_{SAT}\cdot\left(R_2+\frac{R_2+R_3}{\beta}\right)\tag{10}\\\\ \text{Then: }V_{BE} &= V_Z + V_2 - n\: V_T\: \operatorname{LambertW}{\left [\frac{V_Z}{n \:V_T} \cdot e^{\frac{V_Z + V_2}{ n\: V_T} } \right ]}\tag{11}\end{align*}$$
The above applies for active mode. And in this case, \$\beta\$ is now another model parameter you need to estimate for the device. (It depends on temperature and \$V_{BE}\$ [or, alternatively, \$I_C\$.])
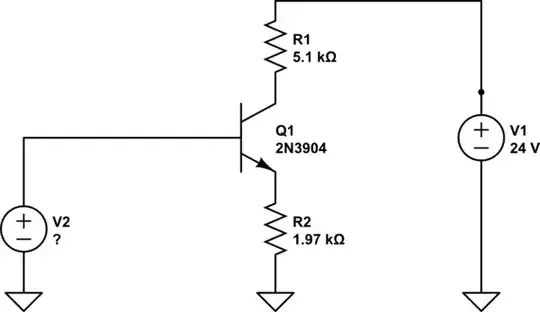
For example, in the above circuit case if we set \$R_2=1.97\:\text{k}\Omega\$ and \$R_3=0\:\Omega\$ (you don't show it in your schematic) and assume that \$V_T\approx 26\:\text{mV}\$ and \$n=1\$ (typical for small signal devices) and \$I_{SAT}=20\:\text{fA}\$ (also typical for small signal devices), then if I also set \$V_2=3\:\text{V}\$ I will compute \$V_{BE}\approx 645 \:\text{mV}\$ for the \$\beta=200\$ case.
From there, the rest can be easily estimated.
Of course, the value of \$\beta\$ is assumed to be in an active mode and a relatively nominal value of \$200\$. If the BJT is saturated, then this estimate is, of course, wrong. You can easily verify, as a second step, whether or not this assumption is true.
With \$V_{BE}\approx 645 \:\text{mV}\$ and equation (8) above, we'd find \$I_C\approx 1.19\:\text{mA}\$. Then the voltage drop across your collector resistor would be \$1.19\:\text{mA}\cdot 5.1\:\text{k}\Omega\approx 6.07\:\text{V}\$. So the collector would be close to about \$18\:\text{V}\$. And so the BJT isn't saturated and the assumption holds.
Suppose \$\beta=145\$ for a particular BJT. The change would be, \$\Delta V_{BE}\approx -48.5\:\mu\text{V}\$. Not much, as you can see. Of course, you've got a nice voltage source at the base. If the series impedance at the base were, say, \$10\:\text{k}\Omega\$ then the \$\Delta V_{BE}\approx -286\:\mu\text{V}\$ and is larger in magnitude.
You can broadly assume collector current equals emitter current.
Next, you can assume that the emitter voltage equals the base input voltage minus 0.7 volts. So you choose the input voltage and emitter resistance to give you the current needed in the collector.
So if your collector current is 3.4 mA then this also (largely) flows through the emitter resistance of 1.97 kohm and therefore the emitter voltage has to be 6.7 volts. This means that to get approximately that voltage at the emitter, the base voltage needs to be 0.7 volts higher at 7.4 volts.
Still you can find the collector current using the well-known equation \$I_c=I_se^{Vbe/Vt}\$ if you at least know Is and Vt. The base-emitter voltage Vbe can be found as such:
$$V_{be}=V_2 -I_cR_2$$
(assuming collector and emitter currents are equal). Using a method called recursion you can find the collector current by first assuming a initial value for the collector current. Make an educative guess and work your way from there. The equation for the collector current then becomes
$$Ic_{n+1}=I_s e^{(V_2 -Ic_nR_2)/Vt}$$
So if you pick \$Ic_1\$=3.1mA you can put this into the above equation and find \$Ic_2\$. Then put \$Ic_2\$ in the eqation and find \$Ic_3\$. This is what recursion means. Continue this until \$|Ic_{i+1}-Ic_i| < \epsilon \$, where \$\epsilon\$ is a very small number depending on the level of accuracy you want. Now, \$Ic_i\$ is the current of the collector to within some accuracy.
Though the above approach is feasible this is not too handy to work it out. There is a much simpler way to do it as stated by others above. I still don't know if that's the kind of approach you want to follow. Anyway, this is how Ebers-Moll equation goes.
