How to calculate the total resistance of this electrical circuit

Question

I'm a programmer and I'm making an Artificial Intelligence for a boardgame called Hex. Since I am not that familiar with electrical engineering, I need your expertise on this subject.

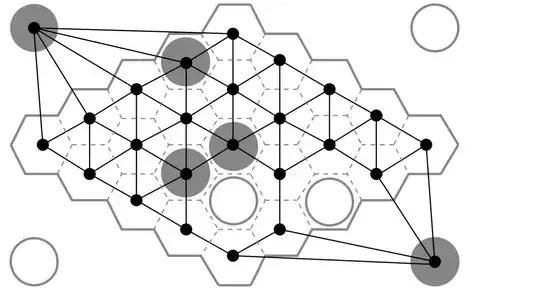
I am now working on the evaluation function of the board. I have represented the board as a graph, since that is what a computer needs as input. But in this case you can also see it as an electrical circuit. The circuit usually looks like this, only then 11x11 hexagons:

The edges/resistors are all either 0,1 or INF (infinity).

My goal is to give a score to the board. I want to apply an electrical voltage to the two boundary opposite nodes and then check the total resistance between them.

I have made a possible scenario on a 2x2 board. The dots are nodes, the edges are resistors, the numbers the resitor values, and the arrows are my current-stream assumptions: 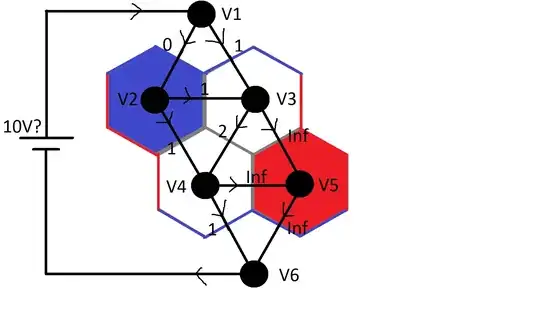So the way I understand it is, I have to do something called nodal analysis. So i made for each node an equation where the voltage going in a node is the same as going out. So here are the equations I made:

$$V1 : \frac{(V1-V2)}{0} + \frac{(V1-V3)}{1} = 10 $$ (From what I understand the voltage source number doesn't matter so I picked 10).

$$V2:\frac{(V1-V2)}{0} = \frac{(V1-V3)}{1} + \frac{(V2-V4)}{1}$$

$$V3: \frac{V1-V3}{1} + \frac{(V2-V3)}{1} = \frac{(V3-V4)}{2} + \frac{(V3-V5)}{\infty}$$

$$V4: \frac{(V2-V4)}{1} + \frac{(V3-V4)}{2} = \frac{(V4-V5)}{\infty} + \frac{(V4-V6)}{1}$$

$$V5: \frac{(V3-V5)}{\infty} + \frac{(V4-V5)}{\infty} = \frac{(V5-V6)}{\infty}$$

$$V6: \frac{(V4-V6)}{1} + \frac{(V5-V6)}{\infty} = 10? $$ (I assume the current leaving out here is 10, but I'm not entirely sure)

So with some algebraic manipulations I put the numbers into a matrix, where the voltages are the variables ofcourse: (I also assumed dividing by zero is the same as multiplying by Infinity, I don't know if that is the correct way).

$$\infty -\infty -1 0 0 0 = 10$$

$$\infty -\infty 1 1 0 0 = 0$$

$$1 1 -2.5 0.5 0 0 = 0$$

$$0 1 0.5 -2.5 0 1 = 0$$

$$0 0 0 0 0 0 = 0 $$

$$0 0 0 1 0 -1 = 10 (?)$$

If you solve this you get:

$$V1: NaN $$
$$V2: NaN $$
$$V3: 0.05 $$
$$V4: 0.05 $$
$$V5: 0 $$
$$V6: -0.05$$

I have two questions now:

1.Where is my mistake in? (because I don't think voltages can be NaN or negative)

2.If I calculated these voltages correctly, how do I then compute the total resistance?

Answer 1

Set node \$V_6=0\:\textrm{V}\$, to start. (It's convenient and you get to do this exactly once; for any node you want.) Also note that \$V_1=V_2\$, so when you are looking for edges you will need to find all edges emanating from all such shared "super" nodes. (So \$V_2\$ won't appear below.) I also notice that your smaller example has a "2" as the value for an edge, when I think you earlier said that only 0, 1, or \$\infty\$ was possible. I'll live with that, though.

So the summary here is: (1) that nodes connected by 0 are the same node and you have to find all edges emanating from the same node when setting up the equations; and, (2) that edges with \$\infty\$ can be ignored; and, (3) fractions with the special node you designate as 0 in the numerator can be dropped.

Note that \$V_5\$ is, in effect, an isolated vertex. So you won't be able to compute a voltage for it. That should be fine. Also, you make have a leaf vertex (I wouldn't know how you deal with making your graph.) The voltage there will be unknown if the edge is \$\infty\$ and will be equal to the voltage at the connected node, otherwise. I'd probably just set it equal, in such cases, and be done with it.

Finally, I won't other with the \$\Omega\$ symbol (you can assume it, if you want.) Instead, I'll use the edge notation of \$R_{23}\$, for example, to represent the indicated edge resistance. If a node is shared, I'll use \$V_{12}\$, for example, to indicate that super node. Your example set of equations is:

---

$$\begin{align*} \frac{V_{12}}{R_{13}}+\frac{V_{12}}{R_{23}} + \frac{V_{12}}{R_{24}} &= \frac{V_3}{R_{13}} + \frac{V_3}{R_{23}} + \frac{V_4}{R_{24}}\\\\ \frac{V_3}{R_{13}}+\frac{V_3}{R_{23}} + \frac{V_3}{R_{34}} &= \frac{V_{12}}{R_{13}} + \frac{V_{12}}{R_{23}} + \frac{V_4}{R_{34}} \\ \\ \frac{V_4}{R_{24}}+\frac{V_4}{R_{34}} + \frac{V_4}{R_{46}} &= \frac{V_{12}}{R_{24}} + \frac{V_3}{R_{34}} \end{align*}$$

---

The above can be converted to:

$$\begin{align*} V_{12}\cdot\frac{1}{R_{13} \vert\vert R_{23} \vert\vert R_{24}} + V_3\cdot\frac{-1}{R_{13}\vert\vert R_{23}} + V_4\cdot\frac{-1}{R_{24}} &= 0\\\\ V_{12}\cdot\frac{-1}{R_{13}\vert\vert R_{23}} + V_3\cdot\frac{1}{R_{13}\vert\vert R_{23}\vert\vert R_{34}}+V_4\cdot\frac{-1}{R_{34}} &= 0 \\ \\ V_{12}\cdot\frac{-1}{R_{24}} + V_3\cdot\frac{-1}{R_{34}} + V_4\cdot\frac{1}{R_{24}\vert\vert R_{34}\vert\vert R_{46}} &= 0 \end{align*}$$

From the above, the symmetries should now also be obvious. (Look at the constants and their positions.) The main diagonal has unique values, but the rest have values that appear twice in easily noticed symmetric positions.

---

But you don't need the first equation, since you already know the value of \$V_{12}\$. So it all boils down to just the bottom two equations converted to matrix form:

$$\begin{align*} V_3\cdot\frac{1}{R_{13}\vert\vert R_{23}\vert\vert R_{34}}+V_4\cdot\frac{-1}{R_{34}} &= V_{12}\cdot\frac{1}{R_{13}\vert\vert R_{23}} \\ \\ V_3\cdot\frac{-1}{R_{34}} + V_4\cdot\frac{1}{R_{24}\vert\vert R_{34}\vert\vert R_{46}} &= V_{12}\cdot\frac{1}{R_{24}} \end{align*}$$

The above solves out in your case as \$V_3=9\frac{1}{6}\:\textrm{V}\$ and \$V_4=5\frac{5}{6}\:\textrm{V}\$.

---

Solved for the node voltages, you can figure out the current by simply examining all the edges leaving from your node 0 (if you pick it the way I did.) There's only one edge there, namely \$R_{46}\$, so the total resistance here is simply \$R_{total}=\frac{V_{total}}{I_{total}}=\frac{V_{12}}{\left[\frac{V_4}{R_{46}}\right]}=R_{46}\cdot\frac{V_{12}}{V_4}\$.

That works out to \$1\frac{5}{7}\:\Omega\$.

---

You should be able to generalize the above, as it's almost already close to automatic.

Answer 2

I think there is a more systematic way to solve circuits, for example you might formalize a way to write the net-list of your circuit and then implement [for example] the MNA algorithm to solve the whole circuit for you,and then you can get the circuit equivalent resistance or any other parameter of interest. I have found a python library called ahkab that implements the modified nodal analysis algorithm. in case you wanted to implement it you might want to check this

I have written a small script that reads the net-list of these hexagon circuit nodes and do the calculation for the equivalent resistance.

The net-list format looks something like this [you can make your own format]

v 1 6 10

1 1 3

0 1 2

1 2 3

1 2 4

2 3 4

1 4 6

end

the first line indicates that the voltage source is connected between node 1 and 6 while all the other lines indicates the value of the resistances and where they are connected to <Resistor value> <Node1> <Node2> and end to finish reading the net-list

Script in python 3

import ahkab
ckt=ahkab.Circuit("Math_Max circuit")
nodes=[]
gnd=0
rCount=0
def node_replace(a,b):
    #A function for replacing 0 resistive path between nodes        
    for i in range(len(nodes)):
        if(nodes[i][1]==a):
            nodes[i][1]=b
        if(nodes[i][2]==a):
            nodes[i][2]=b

while(True):
    nlst=input().split()
    if(nlst[0]=='end'): break
    if(nlst[0]=='v'):
        gnd=int(nlst[2])
        ckt.add_vsource(nlst[0],nlst[1],ckt.gnd,dc_value=int(nlst[3]))
    else:
        nodes.append([int(nlst[0]),nlst[1],nlst[2]])

for i in range(len(nodes)):
    if(nodes[i][0]==0):
        node_replace(nodes[i][2],nodes[i][1])

for i in range(len(nodes)):
    if(nodes[i][0]!=0):
        gndNode=nodes[i][2]
        if(int(nodes[i][2])==gnd):
            gndNode=ckt.gnd
        ckt.add_resistor('r'+str(rCount),nodes[i][1],gndNode,value=nodes[i][0])
        rCount=rCount+1

results=ahkab.run(ckt, ahkab.new_op())['op']
print("TOTAL CURRENT: ",results['I(V)'][0][0])
print("Equivalent resistance: ",10/abs(results['I(V)'][0][0]))

This was the result

The code works by evaluating the total current using the MNA algorithm and then divide the source voltage / total current in order to get the equivalent resistance.