This is not homework.
Imagine an infinite resistor grid which the picture shows a part of. The question is what's the resistance measured across any of the 1k\$\Omega\$ resistors. I don't want you to tell me the answer, I already know. I want to know how to find the solution. I wish I could show where I got so far, but I'm afraid I don't even get started.
To anyone who wants to try for himself, and doesn't want to know the solution: don't click the link to the solution.
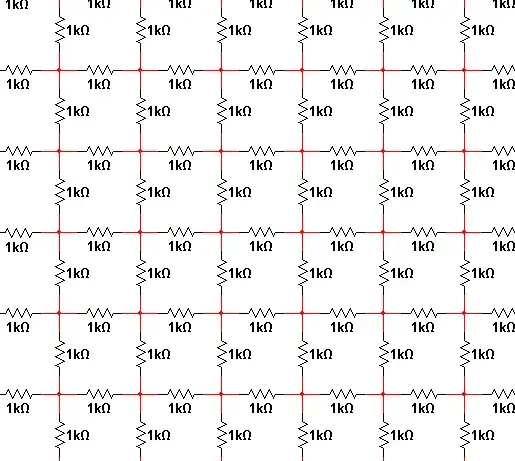
This is a recursive infinite series problem. You can start by considering only one strip with two rows of horizontal resistors and one row of vertical between them. Pick one of the vertical resistor and imagine the current that flows when 1V is put accross it. Note that the infinite strips on either side will contribute to the same current and are independent, so you solve for only one side and double the result. Now write the infinite series with a new term each new vertical resistor. With that you can solve the original infinite strip. Similar technique, althoug a bit more complicated, will let you add a infinite number of strips.
Numerically, you could make this a sufficiently large grid so that current in the edge resistors are below so small as to not matter for the desired accuracy. Now put a fixed voltage accross one resistor and perform iterative relaxation on the voltage and currents in the grid. After this settles sufficiently, you have the total current drawn when 1V is applied accross a single resistor, from which you can compute its the effective resistance.
