3

I am trying to understand the neural network architecture used by Ho et al. in "Denoising Diffusion Probabilistic Models" (paper, source code). They include self-attention layers in the model, applying them to the feature maps output by previous convolutional layers (ResNet blocks). I understand self-attention in the context of sequential data, but here there is no sequence of vectors, just a single image to be processed by self-attention. I do not understand what the self-attention layer is doing to the feature maps.

Question: please could you explain the function of the self-attention layers in this CNN?

My guess is that the self-attention layer is treating pixels like sequence elements i.e. it uses keys/queries to find the pixels in the input feature map that are most relevant to the pixel at some spatial location in the input feature map, then forms a relevance weighted sum of these pixels (or rather their corresponding values) as the output at that location. But this perspective doesn't seem to be consistent with the mechanics of the operation. In sequential data, we have Q, K, V matrices which store embeddings pertaining to the different sequence elements as different rows in the matrices, and it seems that we're replacing these with Q, K, V matrices that are derived from a single image. So when we e.g. calculate $QK^\top$ we are not computing the dot-product similarity of the queries and keys of different elements=pixels, because a row of $Q$ and a row of $K$ does not correspond to one element=pixel in the image (contrast to sequential data where they would correspond to specific sequence elements).

Note: from reading the paper/source code, I think that the self-attention operation is working according to the diagram below, but please correct me if this isn't the case. 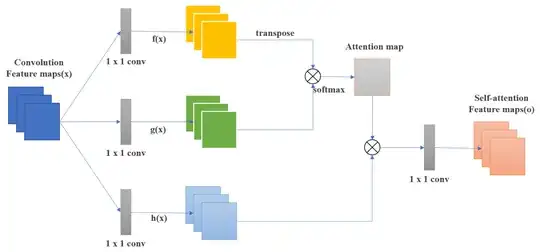self attention operation on feature maps (Figure reproduced from this paper and a similar set-up can be found in the self-attention GAN paper.)

Rational Function
  • 151
  • 4

1 Answers1

2

The implementation of self-attention in the source code for the "Self-Attention Generative Adversarial Networks" (SAGAN) paper is somewhat easier to follow than that in the "Denoising Diffusion Probabilistic Models" paper. Assuming that both papers are using the same approach to self-attention on feature maps (which I think they are), the question can be answered by inspecting the definition of self-attention used in SAGAN:

class Self_Attn(nn.Module):
""" Self attention Layer"""
def __init__(self,in_dim,activation):
    super(Self_Attn,self).__init__()
    self.chanel_in = in_dim
    self.activation = activation

    self.query_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
    self.key_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
    self.value_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim , kernel_size= 1)
    self.gamma = nn.Parameter(torch.zeros(1))

    self.softmax  = nn.Softmax(dim=-1) #
def forward(self,x):
    """
        inputs :
            x : input feature maps( B X C X W X H)
        returns :
            out : self attention value + input feature 
            attention: B X N X N (N is Width*Height)
    """
    m_batchsize,C,width ,height = x.size()
    proj_query  = self.query_conv(x).view(m_batchsize,-1,width*height).permute(0,2,1) # B X CX(N)
    proj_key =  self.key_conv(x).view(m_batchsize,-1,width*height) # B X C x (*W*H)
    energy =  torch.bmm(proj_query,proj_key) # transpose check
    attention = self.softmax(energy) # BX (N) X (N) 
    proj_value = self.value_conv(x).view(m_batchsize,-1,width*height) # B X C X N

    out = torch.bmm(proj_value,attention.permute(0,2,1) )
    out = out.view(m_batchsize,C,width,height)

    out = self.gamma*out + x
    return out,attention

The calls of .view(m_batchsize,-1, width*height) in the forward pass are flattening the spatial image dimensions from (W,H) to (N,) where N=H*W, so the 2D array of pixels in the feature map is being converted into a 1D sequence of pixels, then self-attention is being computed over these sequence elements in the usual manner. So the guess in the question is correct; self-attention is being computed in a pixel-wise manner, and the complaints following the guess are resolved when flattening the feature maps before computing self-attention.

Rational Function
  • 151
  • 4