What does the temperature parameter mean when talking about the GPT models?
I know that a higher temperature value means more randomness, but I want to know how randomness is introduced.
Does temperature mean we add noise to the weights/activations or do we add randomness when choosing a token in the softmax layer?
In sequence generating models, for vocabulary of size $N$ (number of words, parts of words, any other kind of token), one predicts the next token from distribution of the form: $$ \mathrm{softmax} (x_i/T) \quad i = 1, \ldots N, $$ Here $T$ is the temperature. The output of the softmax is the probability that the next token will be the $i$-th word in the vocabulary.
The temperature determines how greedy the generative model is.
If the temperature is low, the probabilities to sample other but the class with the highest log probability will be small, and the model will probably output the most correct text, but rather boring, with small variation.
If the temperature is high, the model can output, with rather high probability, other words than those with the highest probability. The generated text will be more diverse, but there is a higher possibility of grammar mistakes and generation of nonsense.
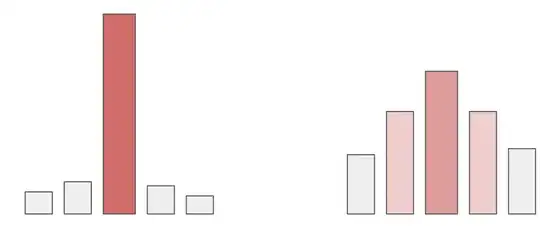
The difference between the low-temperature case (left) and the high-temperature case for the categorical distribution is illustrated in the picture above, where the heights of the bars correspond to probabilities.
Example
A good sample is provided in the Deep Learning with Python by François Chollet in chapter 12. An extract from the tutorial, refer to this notebook.
import numpy as np
tokens_index = dict(enumerate(text_vectorization.get_vocabulary()))
def sample_next(predictions, temperature=1.0):
predictions = np.asarray(predictions).astype("float64")
predictions = np.log(predictions) / temperature
exp_preds = np.exp(predictions)
predictions = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, predictions, 1)
return np.argmax(probas)
