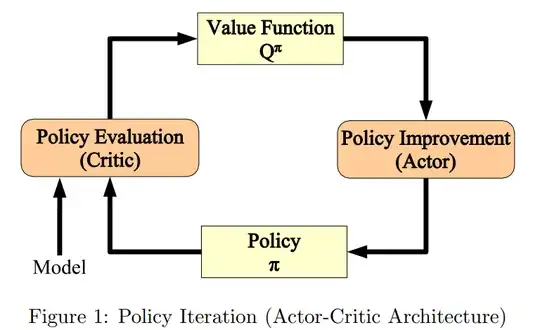
Value iteration (VI) is a truncated version of Policy iteration (PI).
PI has two steps:
- the first step is policy evaluation. That is to calculate the state values of a given policy. This step essentially solves the Bellman equation
$$v_\pi=r_\pi+\gamma P_\pi v_\pi$$
which is the matrix vector form of the Bellman equation. I assume that the basics are already known.
- The second is policy improvement. That is to select the action corresponding to the greatest action value at each state (i.e., greedy policy):
$$\pi=\arg\max_\pi(r_\pi+\gamma P_\pi v_\pi)$$
The key point is: the policy iteration step requires an infinite number of iterations to solve the Bellman equation (i.e., get the exact state value).
In particular, we use the following iterative algorithm so solve the Bellman equation:
$$v_\pi^{(k+1)}=r_\pi+\gamma P_\pi v_\pi^{(k)}, \quad k=1,2,\dots$$
We can prove that $v_\pi^{(k)}\rightarrow v_\pi$ as $k\rightarrow\infty$.
There are three cases to execute this iterative algorithm:
- Case 1: run an infinite number of iterations so that $ v_\pi^{(\infty)}=v_\pi$. This is impossible in practice. Of course, in practice, we may run sufficiently many iterations until certain metrics (such as the difference between two consecutive values) are small enough).
- Case 2: run just one single step so that $ v_\pi^{(2)}$ is used for policy improvement step.
- Case 3: run a few times (e.g., N times) so that $ v_\pi^{(N+1)}$ is used for the policy improvement step.
Case 1 is the policy iteration algorithm; case 2 is the value iteration algorithm; case 3 is a more general truncated version. Such a truncated version does not require infinite numbers of iterations and can converge faster than case 2, it is often used in practice.