Suitable reward function for trading buy and sell orders

Question

I am working to build a deep reinforcement learning agent which can place orders (i.e. limit buy and limit sell orders). The actions are {"Buy": 0 , "Do Nothing": 1, "Sell": 2}.

Suppose that all the features are well suited for this task. I wanted to use just the standard "Profit & Loss" as a reward, but I hardly thought to get something similar to the above image. The standard P&L will simply place the pair (limit buy order, limit sell order) on every up movement. I don't want that because very often it won't cover the commission and it is not a good indicator to trade manually. I would be interested that the agent can maximize the profit and give me a minimum profit of $100 on every pair (limit buy order, limit sell order).

I would be interested in something similar to the picture below.

Is there a reward function that could allow me to get such a result? If so, what is it?

UPDATE

Is the following utility function can work with the purpose of that question?

$$ U(x) = \max(\\\$100, x) $$

That seems correct, but I don't know how the agent will be penalized if it covers a wrong transaction, i.e. the pair (limit buy order, limit sell order) creates a loss of money.

Answer 1

Generally researchers (Ghandar et al, Michalewicz, Lam) have used the profit or return on investment (ROI) as a reward (fitness) function.

$ROI = \frac{ \left[\sum_{t=1}^T (Price_t - sc) \times I_s(t) \right] - \left[ \sum_{t=1}^T (Price_t + bc) \times I_b(t) \right] }{ \left[ \sum_{t=1}^T (Price_t + bc) \times I_b(t) \right] }$

where $I_b(t)$ and $I_s(t)$ are equal to one if a rule signals a buy and sell, respectively, and zero otherwise; $sc$ represents the selling cost and $bc$ the buying cost. ROI is the difference between final bank balance and starting bank balance after trading.

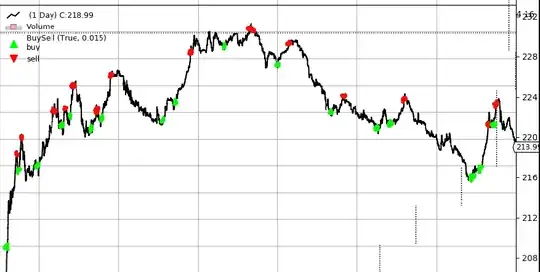
You are correct, that the machine learning algorithm will then be influenced by spikes just before a sell.

Nicholls et al showed that using the average profit or area under the trade resulted in better performing trading rules. This approach was used by Schoreels et al. This approach focuses on being in the market to capitalize on profit. It does not penalize the trading rule when it is in the market and the market is going down. The accumulated asset value (AAV) is defined as:

$AAV = \frac{\sum_{i=1}^N [(Price_s - sc) - (Price_b + bc)]}{N}$

where $i$ is a buy and sell trading event, $N$ is the number of buy and sell events, $s$ the day the sale took place, and $b$ is the day the purchase took place.

Nicholls MSc thesis [available April 2019] showed that the fitness function used by Allen and Karjalainen is the preferred fitness function when evolving trading rules for the JSE using evolutionary programs.

Allen and Karjalainen used a fitness function based on the compounded excess returns over the buy-and-hold (buy the first day, sell the last day) strategy. The excess return is given by:

$\Delta r = r - r_{bh}$

where the continuously compounded return of the trading rule is computed as

$r = \sum_{t=1}^T r_i I_b(t) + \sum_{t=1}^T r_f I_s(t) + n\log\left(\frac{1-c}{1+c'}\right)$

and the return for the buy-and-hold strategy is calculated as

$r_{bh} = \sum_{t=1}^T r_t + \log\left(\frac{1-c}{1+c'}\right)$

In the above,

$r_i = \log P_t - \log P_{t-1}$

and $P$ is the daily close price for a given day $t$, $c$ denotes the one-way transaction cost; $r_f$ is the risk free cost when the trader is not trading, $I_b(t)$ and $I_s(t)$ are equal to one if a rule signals buy and sell, respectively, and zero otherwise; $n$ denotes the number of trades and $r_{bh}$ represents the returns of a buy-and-hold, while $r$ represents the returns of the trader.

A fixed trading cost of $c = 0.25\%$ of the transaction was defined but this could be anything like a STATE fee + Brocker fee + Tax, and might even be 2 different values, one for buying and one for selling. Which was the approach used by Nicholls. The continuously compounded return function rewards an individual when the share value is dropping and the individual is out of the market. The continuously compounded return function penalises the individual when the market is rising and the individual is out of the market.

I would recommend that you use the compounded excess return over the buy and hold strategy as your reward function.