Matrix/Stochastic/Introduction/Section

Definition

A real square matrix

{}M={\left(a_{ij}\right)}_{1\leq i,j\leq n}\,

is called column stochastic matrix if all entries

{}a_{ij}\geq 0\,,

and every column sum (that is, for every ${}j$ ), is

{}\sum _{i=1}^{n}a_{ij}=1\,.

The basic interpretation for a column stochastic matrix is the following: There is a set of ${}n$ possible places, spots, positions, vertices in a network, web pages, etc., where someone or something can be with a certain probability (a distribution, a weighting). Such a distribution is described by an ${}n$ -tuple ${}{\begin{pmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{pmatrix}}$ with real non-negative numbers ${}v_{i}$ satisfying ${}\sum _{i=1}^{n}v_{i}=1$ . This is also called a distribution vector. A column stochastic matrix describes the transition probability in the given network in a certain time segment. The entry ${}a_{ij}$ is the probability that an object being at the vertex ${}j$ (a visitor of the web page ${}j$ ) moves to the position ${}i$ (goes to the webpage ${}i$ ). The ${}j$ -th standard vector corresponds to the distribution where everything is in the vertex ${}j$ .The ${}j$ -th column of the matrix describes the image of this standard vector under the matrix. In general, for a given distribution ${}v$ , applying the matrix computes the image distribution ${}Mv$ ; see exercise. A natural question is whether there are distributions that are stationary (stationary distribution, or fixed distribution, or eigendistribution), that is, they are transformed to themselves, or whether there exist periodic distributions, or whether there exist limit distributions, and how to compute them.

Example

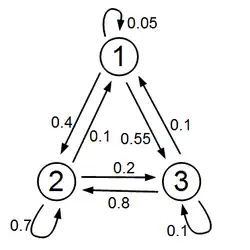
A column stochastic ${}2\times 2$ -matrix has the form

{\begin{pmatrix}p_{1}&p_{2}\\1-p_{1}&1-p_{2}\end{pmatrix}}

wit

{}0\leq p_{1},p_{2}\leq 1\,.

The characteristic polynomial is

{}{\begin{aligned}(X-p_{1})(X-1+p_{2})-(1-p_{1})p_{2}&=X^{2}+(p_{2}-p_{1}-1)X+p_{1}(1-p_{2})-p_{2}(1-p_{1})\\&=X^{2}+(p_{2}-p_{1}-1)X+p_{1}-p_{2}\\&=(X-1)(X+p_{2}-p_{1}).\,\end{aligned}}

Eigenvalues are ${}1$ and ${}p_{1}-p_{2}$ . A stationary distribution is (exclude the cases ${}p_{1}=1$ and ${}p_{2}=0$ for the following computation) given by ${}{\begin{pmatrix}{\frac {p_{2}}{p_{2}-p_{1}+1}}\\{\frac {1-p_{1}}{p_{2}-p_{1}+1}}\end{pmatrix}}$ , because of

{}{\begin{aligned}{\begin{pmatrix}p_{1}&p_{2}\\1-p_{1}&1-p_{2}\end{pmatrix}}{\begin{pmatrix}{\frac {p_{2}}{p_{2}-p_{1}+1}}\\{\frac {1-p_{1}}{p_{2}-p_{1}+1}}\end{pmatrix}}&={\begin{pmatrix}p_{1}{\frac {p_{2}}{p_{2}-p_{1}+1}}+p_{2}{\frac {1-p_{1}}{p_{2}-p_{1}+1}}\\(1-p_{1}){\frac {p_{2}}{p_{2}-p_{1}+1}}+(1-p_{2}){\frac {1-p_{1}}{p_{2}-p_{1}+1}}\end{pmatrix}}\\&={\begin{pmatrix}{\frac {p_{1}p_{2}+p_{2}(1-p_{1})}{p_{2}-p_{1}+1}}\\{\frac {(1-p_{1})p_{2}+(1-p_{2})(1-p_{1})}{p_{2}-p_{1}+1}}\end{pmatrix}}\\&={\begin{pmatrix}{\frac {p_{2}}{p_{2}-p_{1}+1}}\\{\frac {1-p_{1}}{p_{2}-p_{1}+1}}\end{pmatrix}}.\end{aligned}}

Example

The column stochastic ${}2\times 2$ -matrix

{\begin{pmatrix}0&1\\1&0\end{pmatrix}}

transforms the distribution ${}{\begin{pmatrix}p\\1-p\end{pmatrix}}$ into the distribution ${}{\begin{pmatrix}1-p\\p\end{pmatrix}}$ . The contribution ${}{\begin{pmatrix}{\frac {1}{2}}\\{\frac {1}{2}}\end{pmatrix}}$ is transformed to itself, that is, it is a stationary distribution. The distribution ${}{\begin{pmatrix}1\\0\end{pmatrix}}$ is transformed into ${}{\begin{pmatrix}0\\1\end{pmatrix}}$ , and vice versa. It is a periodic distribution, the period length is ${}2$ .

Example

The column stochastic ${}n\times n$ -matrix

{\begin{pmatrix}1&1&\cdots &1\\0&0&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &0\end{pmatrix}}

transforms the distribution ${}{\begin{pmatrix}v_{1}\\\vdots \\v_{n}\end{pmatrix}}$ into the distribution

{}{\begin{pmatrix}1&1&\cdots &1\\0&0&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &0\end{pmatrix}}{\begin{pmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{pmatrix}}={\begin{pmatrix}\sum _{i=1}^{n}v_{i}\\0\\\vdots \\0\end{pmatrix}}={\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}\,.

The first standard vector is an eigenvector of the eigenvalue ${}1$ ; every other standard vector, and in fact every distribution vector, is transformed into the first standard vector. The kernel is generated by the vectors ${}e_{1}-e_{j}$ , ${}j\geq 2$ , and does not contain any distribution vector.

Example

Let ${}N$ be a network (a "directed graph“), consisting in a set ${}K$ of vertices, and a set of directed edges, which can exist between the vertices. For example, ${}K$ is the set of all web pages, and there exists an arrow from ${}j\in K$ to ${}i\in K$ , if the web page ${}j$ has a link to the web page ${}i$ . The linking structure can be expressed by the adjacency matrix

{}A={\left(a_{ij}\right)}\,,

where

{}a_{ij}:={\begin{cases}1,\,{\text{there exists a link from }}j{\text{ to }}i,\\0,\,{\text{ else}},\end{cases}}\,,

or by the column stochastic matrix

{}B={\left(b_{ij}\right)}\,,

where

{}b_{ij}={\frac {a_{ij}}{d_{j}}}\,,

and ${}d_{j}$ is the number of links starting at the vertex ${}j$ . This division ensures that the column sum equals ${}1$ (we suppose that there is at least one link starting at any vertex).

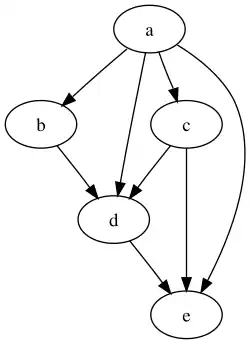
The adjacency matrix, and the column stochastic version of the adjacency matrix of the graph on the right (where we add always self links) are

{\begin{pmatrix}1&0&0&0&0\\1&1&0&0&0\\1&0&1&0&0\\1&1&1&1&0\\1&0&1&1&1\end{pmatrix}}{\text{ and }}{\begin{pmatrix}{\frac {1}{5}}&0&0&0&0\\{\frac {1}{5}}&{\frac {1}{2}}&0&0&0\\{\frac {1}{5}}&0&{\frac {1}{3}}&0&0\\{\frac {1}{5}}&{\frac {1}{2}}&{\frac {1}{3}}&{\frac {1}{2}}&0\\{\frac {1}{5}}&0&{\frac {1}{3}}&{\frac {1}{2}}&1\end{pmatrix}}.