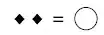4

Recently, I started to study practical application of ZX calculus but I am confused by meaning of "diamond" and "loop".

Issue no. 1: There are these rules:

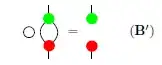
B-rule

b-rule

and D-rule

d-rule

But this example seems to use the rules wrongly:

Example 1

In the middle of a digram, B-rule is used, however, I do not see any loop or diamonds justifying this step (i.e. a disconection of nodes).

Similar situation occurs in this example:

Example 2

Why is it possible to ignore loop and diamonds?

Issue no. 2:

Interpreation of a diamond in Hilbert space is this:

Diamond = $\sqrt{2}$

What does mean that diamond is $\sqrt{2}$? Is it a normalization constant?

Interpreation of a loop in Hilbert space is this:

Loop represent the dimension of underlying Hilbert space

Assuming D-rule, loop should represent two diamonds hence $\sqrt{2}\sqrt{2} = 2$ which is dimension of Hilbert space for description of single qubit states. But ZX calculus can be used for any number of qubits. What does it mean that loop represent a dimension? How is a dimension of "multi-qubits" Hilbert space represented?

Martin Vesely
  • 15,244
  • 4
  • 32
  • 75

1 Answers1

2

  1. If you agree to treat diagrams up to a constant factor, then you can ignore loops and diamonds. As you correctly guessed, it's a normalization constant.

  2. For a multi-qubit system, you represent an identity operator with several wires. If you trace them, you get dimension equal to $2^n$, and in the diagram you represent this dimension as $n$ disjoint loops each contributing a factor of 2.

Alexey Uvarov
  • 716
  • 5
  • 15