How to prepare Unitary Coupled Cluster ansatz for VQE in a circuit?

Question

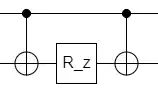
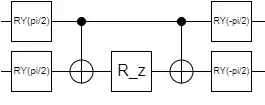
I have read the following paper by Dumitrescu et al.

To make a Unitary Coupled Cluster (UCC) ansatz, one prepares with the following equation. $$ | \psi_{\rm{UCC}} \rangle = U(\theta)|\mathrm{HF}\rangle $$ Here, $U(\theta) = \exp[ T(\theta) - T^{\dagger}(\theta) ]$ and $|\mathrm{HF}\rangle$ is the Hartree-Fock state.

Let me consider a simple system where $T(\theta) = \theta a_0^{\dagger}a_1$. Then one obtains $$\begin{align} U(\theta) &= \exp[ \theta(a_0^{\dagger}a_1 - a_1^{\dagger}a_0) ] \;. \\ &= \exp[ i(\theta/2) (X_0Y_1 - X_1Y_0) ] \end{align} $$

Here, one applies Jordan-Wigner transformation.

So far, I can understand but hereafter how can I make a circuit? Should I expand and calculate $U(\theta)|\mathrm{HF}\rangle$ with Baker-Campbell-Hausdorff formula or something?

Answer 1

You can create the unitary gate for operator $U(\theta)=e^{-i\frac{\theta}{2}Z_{0}Z{1}}$ using two $CNOT$ operations and single rotation gate $R_z$:

For operators which contain different tensor products of Pauli matrices beside the product of $Z$ you have to change basis using appropriate unitary transformation: $R_y(-\frac{\pi}{2})$ changes $X$ basis to $Z$ basis, and $R_{x}(\frac{\pi}{2})$ changes $Y$ basis to $Z$ basis. For example for operator $U(\theta)=e^{-i\frac{\theta}{2}X_{0}X{1}}$ you have the following cirquit: