How to construct a circuit to perform this operation? Is there a general way of getting a circuit from a matrix?

Question

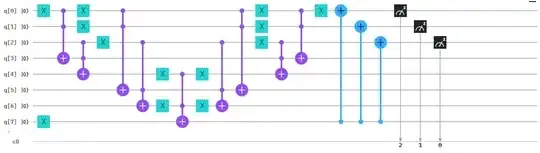
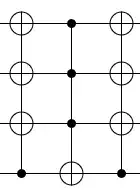
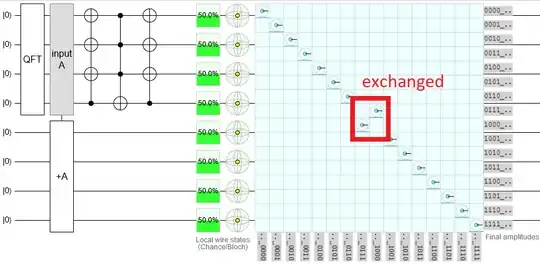
I want to build a circuit that performs the following operation: $$ U_f = \left(\begin{array}{cccccccccc} 1 & 0 & 0 & \dots & \dots & \dots & \dots & \dots & \dots & 0 \\ 0 & 1 & 0 & & & & & & & \vdots\\ 0 & 0 & 1 & & & & & & & \vdots \\ \vdots & & & \ddots & & & & & & \vdots \\ \vdots & & & & 0 & 1 & & & & \vdots \\ \vdots & & & & 1 & 0 & & & & \vdots \\ \vdots & & & & & & \ddots & & & \vdots \\ \vdots & & & & & & & 1 & 0 & 0 \\ \vdots & & & & & & & 0 & 1 & 0 \\ 0 & \dots & \dots & \dots & \dots & \dots & \dots & 0 & 0 & 1 \end{array}\right) $$ but I don't know the equivalent gate combination, and I have never seen such a matrix on any book.

So I am curious about how one could build this circuit, and generally, given a matrix, if there is any general procedure of decomposing it in gates or deriving the circuit.

Answer 1

I investigated your gate for three different cases:

1) one q-bit: in this case the $U_f$ is simply $X$

2) two q-bits: state $|01\rangle$ is mapped to $|10\rangle$ and conversely, otherwise q-bits are unchanged, so the gate implements q-bits swap

3) three or more q-bits: gate $U_f$ act like this: state $|011...1\rangle$ is mapped to $|100...0\rangle$ and conversely. These states are mutually inverse, i.e. to obtain the second one from the first one, it is sufficient to negate all q-bits. The same is true for obtaining the first state from the second one. In all other cases q-bits are unchanged. Thus it is necessary to introduce an indicator that a quantum register is either in state $|011...1\rangle$ or $|100...0\rangle$. The indicator can be Boolean function $f = \bar{q_0}q_1...q_{n-1} + q_0\bar{q_1}...\bar{q}_{n-1}$. It returns $|1\rangle$ for states $|100...0\rangle$ and $|011...1\rangle$, otherwise it returns $|0\rangle$. Note, that ancilla q-bits are needed. After calculation of the indicator, the result is stored in ancilla bit, other ancillas are uncomputed and CNOT gates controlled by the result of the function $f$ are applied on q-bits $|q_0\rangle$, $|q_1\rangle$...$|q_{n-1}\rangle$.

Please find here a figure of a circuit implementing case 3) for three q-bits. Its expansion for more q-bits is straighforward. Note that I tested the circuit on IBM Q simulator and it works.

Answer 2

This operation leaves all computational basis states unchanged, except for the $|0111\dots111\rangle$ and $|1000\dots000\rangle$ states, which it exchanges.

The first thing to do is to make those two states differ in only one bit position. This can be done by applying CNOT operations controlled by one of the differing bit positions targeting all other differing bit positions. We'll do a CNOT from the leftmost bit to all other bits, resulting in:

$|0111\dots111\rangle \rightarrow |0111\dots111\rangle$

$|1000\dots000\rangle \rightarrow |1111\dots111\rangle$

Now our states differ in only one bit position. The operation that swaps these two states while affecting no others is a CC..CCNOT controlled by all of the bit positions where the bits are the same (with a control type matching that bit) and targeting the differing bit position.

We then repeat the CNOTs from earlier in order to return to the original basis.

The final circuit looks like this:

Note that this circuit may be upside down, depending on your bit ordering convention.

We can check it has the right matrix by using Quirk's output display and the state channel duality: