Is there a mistake in the VQE Ansatz in Cirq's tutorial?

Question

I have been going through Cirq's VQE background tutorial and after examining the Ansatz it seems to me that the only layer that actually affects the final measurement is the rot_x_layer. The other layers simply act on the phases and therefore seem to have no impact on the final measurement probabilities.

I've also replicated the example using Quirk and the displays seem to confirm my suspicion.

Additionally I've come across a paper on QAOA that also outlines a solution with a different Ansatz and the Hamiltonian they use though, is slightly different in that the sigma that multiplies the external field h has an x on top instead of a z.

Is this a mistake on Cirq's tutorial or am I missing something fundamental in here?

Answer 1

You're right in the sense that the cost unitary, which is composed of all the $Z$ and $CZ$ gates does not affect the underlying probabilities of measuring a specific state by itself, however when we apply the mixer (the layer of $Rx$ gates), the probabilities are changed, due to these added phases.

Let's look at a basic example, to convince you that changing phases, then applying another layer of gates (like $Rx$) can in fact change the probabilities of the measurement outcomes!

Consider the system of one qubit in an even superposition, where we apply an $S$ gate (which is just the square root of the $Z$ gate), then apply a $Rx(\theta)$ gate:

$$$$

$$\Rightarrow \ Rx(\theta) S \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix} \ = \ \frac{1}{\sqrt{2}} Rx(\theta) \begin{pmatrix} 1 \\ i \end{pmatrix} \ = \ \frac{1}{\sqrt{2}}\begin{pmatrix} \cos \theta/2 & -i\sin \theta/2 \\ -i\sin \theta/2 & \cos \theta/2 \end{pmatrix} \begin{pmatrix} 1 \\ i \end{pmatrix}$$

$$\Rightarrow \frac{1}{\sqrt{2}} \begin{pmatrix} \cos \theta/2 \ + \ \sin \theta/2 \\ i(\cos \theta/2 \ - \ \sin \theta/2) \end{pmatrix}$$

So the probability of measuring each of the outcomes is given as:

$$\text{Pr}(0) \ = \ \frac{1}{2}(\cos \theta/2 \ + \ \sin \theta/2)^2$$ $$\text{Pr}(1) \ = \ \frac{1}{2}(\cos \theta/2 \ - \ \sin \theta/2)^2$$

In most cases, these are not equal! Thus, this is a concrete example of a time when we apply some kind of phase, then a non-commuting mixer, and the probabilities of the different measurement outcomes are changed!

Now consider what happens if we didn't apply the $S$ gate:

$$\Rightarrow \ Rx(\theta) \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \ = \ \frac{1}{\sqrt{2}} Rx(\theta) \begin{pmatrix} 1 \\ 1 \end{pmatrix} \ = \ \frac{1}{\sqrt{2}}\begin{pmatrix} \cos \theta/2 & -i\sin \theta/2 \\ -i\sin \theta/2 & \cos \theta/2 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix}$$

$$\Rightarrow \ \frac{1}{\sqrt{2}} \begin{pmatrix} \cos \theta/2 \ - \ i\sin \theta/2 \\ \cos \theta/2 \ - \ i\sin \theta/2 \end{pmatrix}$$

And the probabilities are:

$$\text{Pr}(0) \ = \ \frac{1}{2} (\cos \theta/2 \ - \ i\sin \theta/2)(\cos \theta/2 \ + \ i\sin \theta/2) \ = \ \frac{1}{2} (\sin^2 \theta/2 \ + \ \cos^2 \theta/2) \ = \ \frac{1}{2}$$ $$\text{Pr}(1) \ = \ \frac{1}{2} (\cos \theta/2 \ - \ i\sin \theta/2)(\cos \theta/2 \ + \ i\sin \theta/2) \ = \ \frac{1}{2} (\sin^2 \theta/2 \ + \ \cos^2 \theta/2) \ = \ \frac{1}{2}$$

So they don't change, no matter what we set $\theta$ to.

If you still don't believe me, let's run a simulation in Quirk!

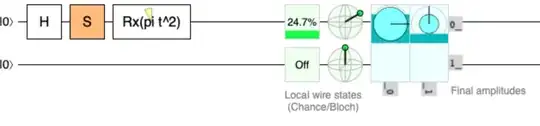
Look at how the probabilities change with different values of $\theta$! It's pretty cool!

Now look what happens without the $S$ gate:

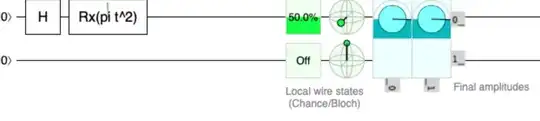
There is no change in the probabilities, thus we require the change in phase for something interesting to happen!

EDIT (IMPORTANT)

The tutorial seems to apply the mixer before the cost unitary, which is strange. To my understanding QAOA should be cost, then mixer, especially if the circuit depth is only $1$.