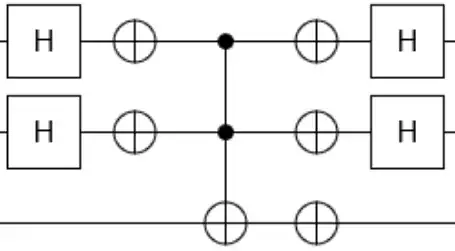
I'm doing a practice assignment where I'm asked to identify specific features of the Grover Search Algorithm's second operator (picture in post, further on "$Us$"), which mirrors the system relative to the $|s\rangle$ vector, defined as the equal-weighted sum of the input parameter's subspace basis vectors (definition below). Naturally, this only concerns the contents of a single iteration.
$$|s\rangle=H|0\rangle^{\otimes n}=\frac{1}{2^{n/2}}\sum_{x=0}^{2^n-1}|x\rangle.$$
The operator is defined by the following scheme, which I have, for reference, built in the Quirk QC simulator.
It has the following proposed features (which I need to verify as true or false):
The Hadamard and NOT gates applied to the qubits 1 and 2 (further on $|C_I\rangle$, $|C_{II}\rangle$) in succession map the $|s\rangle$ vector onto the $|11\rangle$ vector.
The Hadamard and NOT gates applied to the qubits 1 and 2 (further on $|C_I\rangle$, $|C_{II}\rangle$) in succession map the $|s\rangle$ vector onto the $|00\rangle$ vector.
The CNOT gate (with $C_I$ and $C_{II}$ as controls) affects only the $|11C_{III}\rangle$ vector.
The CNOT gate multiplies the $|11C_{III}\rangle$ vector by $-1$ and does not affect other vectors.
The Hadamard, then the NOT gate applied to $C_I$ and $C_{II}$ maps $|11\rangle$ onto $|s\rangle$. The $|s\rangle$ component in the system vector is thus multiplied by $-1$ while components orthogonal to it are unaffected.
The NOT gate on $C_{III}$ multiplies the system vector by $-1$, thus the system vector is reflected relative to $|s\rangle$.
The NOT gate on the $C_{III}$ qubit is unnecessary.
My perspective:
For the first two points, I don't fully grasp the concept of the mapping described here. However, it should be noted that by definition, as far as I understand, the Hadamard transformation on either side of the scheme is to allow the "$Us$" operator to function as a reflection relative to the $|0\rangle^{\otimes n}$ vector.
For (3) and (4), while I have maintained the original wording, I understand the question misnames the CCNOT gate as CNOT - I'm not sure how important this distinction is, other than technically referring to two different types of gates. Both of these are true if only the controlled vector is affected, which I believe to be correct.
I believe (5) is incorrect as, by definition, "$Us$" is a reflection relative to $|s\rangle$. Because of this definition, I believe (6) is correct.
I believe (7) is incorrect because it changes the outcome of the "$Us$" operator.
My understanding of quantum computing is severely limited at the moment, so I'm hoping that I'll be able to gain some much-needed intuition by having my logic here fact-checked.