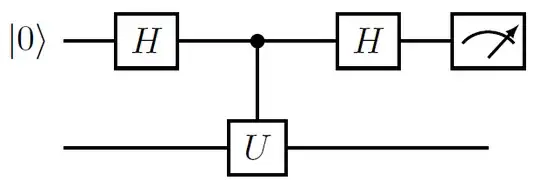
What that cSWAP test does (and doesn't) do
The important thing about the controlled-SWAP test is that what it does isn't just to SWAP, or to not SWAP, the two inputs. The controlled-SWAP test involves a control qubit which is in a superposition of $\def\ket#1{\lvert#1\rangle}\def\bra#1{\langle#1\rvert}\ket{0}$ and $\ket{1}$: that is, we measure the first qubit of the state
$$ \mathrm{cSWAP} \,\Bigl(\ket{+} \otimes \ket{\alpha} \otimes \ket{\beta}\Bigr)$$
in the basis $\ket{+}, \ket{-}$; or to put it in a different way, we measure the first qubit of the state
$$ \bigl(H \otimes \mathbf 1 \otimes \mathbf 1\bigr)\,\mathrm{cSWAP}\,\bigl(H \otimes \mathbf 1 \otimes \mathbf 1\bigr) \,\Bigl(\ket{0} \otimes \ket{\alpha} \otimes \ket{\beta}\Bigr)$$
in the standard basis, to obtain information about how similar $\ket{\alpha}$ and $\ket{\beta}$ are.
Why do we do this? Because what this does is to measure how symmetric the state $\ket{\alpha} \otimes \ket{\beta}$ is.
The cSWAP test as a simulated two-qubit measurement
The SWAP operator is Hermitian: that is, it has eigenvalues ±1. Obviously, any state of the form $\ket{\alpha} \otimes \ket{\alpha}$ is a +1 eigenstate: these span a space of dimension 3, which is spanned by $\ket{0}\ket{0}$, $\ket{1}\ket{1}$, and $\ket{+}\ket{+}$ — or, equivalently, $\ket{00}$, $\ket{11}$, and $\tfrac{1}{\sqrt 2}\bigl(\ket{01} + \ket{10}\bigr)$. The remaining state orthogonal to this space is
$$\ket{\Psi^-} = \tfrac{1}{\sqrt 2}\bigl(\ket{01} - \ket{10}\bigr)$$
which, up to scalar factors, we can equivalently write as
$$\ket{\Psi^-} \propto \tfrac{1}{\sqrt 2}\bigl(\ket{\alpha}\ket{\alpha^\perp} - \ket{\alpha^\perp}\ket{\alpha}\bigr) \,.$$
What the controlled-SWAP test does is to simulate a measurement of $\bigl\{ \Pi_{\textrm{sym}}, \ket{\Psi^-}\!\bra{\Psi^-} \bigr\}$ on the two qubits, where $\Pi_{\textrm{sym}}$ is the projector onto the span of all symmetric states $\ket{\alpha}\ket{\alpha}$ described above.
More specifically, the cSWAP test simulates measurement of the SWAP operator as an observable (as opposed to a unitary transformation). The SWAP operator has eigenvalues ±1, after all — in principle, we can measure the two qubits to see whether they are (or they collapse to) a +1 eigenstate.
The way that the cSWAP test does this is by using cSWAP in place of SWAP, to realise a phase kick, from the two qubits acted on up to the control.
For the eigenstates of SWAP, this records the eigenvalue in the phase of the control; performing a Hadamard then converts this information into a $\ket{0}$ (for symmetric states) or a $\ket{1}$ (for the antisymmetric state $\ket{\Psi^-}$). More generally, it collapses the target states either to the symmetric subspace, or the state $\ket{\Psi^-}$.
The procedure is literally performing a measurement of how symmetric (or antisymmetric) the state is, and producing the result $\ket{0}$ or $\ket{1}$ with some probability accordingly.
The maximum probability of failing the cSWAP test
Considering the procedure in this way, it's easy to see that the maximum probability of obtaining the outcome $\ket{1}$ is 0.5: this is the probability of the state $\ket{\alpha}\ket{\alpha^\perp}$ collapsing to the antisymmetric state $\ket{\Psi^-} \propto \tfrac{1}{\sqrt 2}\bigl(\ket{\alpha}\ket{\alpha^\perp} - \ket{\alpha^\perp}\ket{\alpha}\bigr)$, upon measurement.