The no-cloning theorem states that an unknown quantum state cannot be copied exactly --- so this rules out any algorithm that attempts to produce perfect copies of an arbitrary quantum state (including squeezed and coherent states).
As you note, however, the no-cloning theorem does not rule out the production of approximate quantum state clones. Andersen et al. introduced the most-optimal scheme for cloning of Gaussian states --- their algorithm produces a clone with fidelity of 65% to the original state (the proven optimum possible is $f=2/3$).
The circuit they use in their algorithm is here:
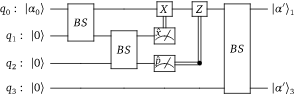
and can be implemented using Strawberry Fields like so:
# state to be cloned
Coherent(0.7+1.2j) | q[0]
# 50-50 beamsplitter
BS = BSgate(pi/4, 0)
# symmetric Gaussian cloning scheme
BS | (q[0], q[1])
BS | (q[1], q[2])
MeasureX | q[1]
MeasureP | q[2]
Xgate(scale(q[1], sqrt(2))) | q[0]
Zgate(scale(q[2], sqrt(2))) | q[0]
# after the final beamsplitter, modes q[0] and q[3]
# will contain identical approximate clones of the
# initial state Coherent(0.1+0j)
BS | (q[0], q[3])
You can check out the Gaussian cloning tutorial in the Strawberry Fields documentation for more information.
