I often wonder if the welded trees considered in the Childs et al. paper have any applicability to questions in algorithmic knot theory such as knot identification/knot canonization. For example, I envision labeling vertices of the welded tree with specific knot diagrams/grid diagrams, and labeling edges with various Reidemeister moves that go from one diagram to another.
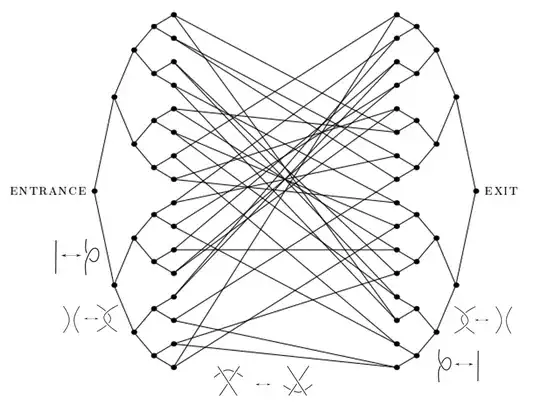
Walking along the tree may be somewhat akin to trying to untangle/untie a complicated knot.
For example, one could identify the $\mathrm{ENTRANCE}$ node with a given knot diagram, and the target $\mathrm{EXIT}$ node with some canonical labeling of the given knot. Each edge corresponds to a Reidemeister move.
- Walking from the left $\mathrm{ENTRANCE}$ to the middle glued region might correspond to performing Reidemeister Type I/II moves that increase the number of crossings, up to an a-priori given maximum crossing number;
- Walking within the middle corresponds to Type III moves that don't change the crossing number but rather just do over/under slides; and
- Walking from the middle to the $\mathrm{EXIT}$ node corresponds to performing Type I/II moves that decrease the crossing number.
I think it's the case that a classical walk to simplify a knot by initially making it more complicated with Type I/II moves often gets stuck doing such Type III moves prior to being able to simplify. Perhaps the quantum walk considered by Childs et al. is more likely to find a simpler canonical knot diagram exponentially faster than a classical walk.
The oracle would be instantiated by labeling a knot diagram/grid diagram (corresponding to the basis states of the Hamiltonian), and providing a list of Reidemeister moves available to such a labeling (corresponding to the off-diagonal elements of the Hamiltonian). Certainly these are classically computable in polynomial time - given a knot diagram, one can enumerate all of the available Reidemeister moves.
As opposed to the tree considered by Childs et al., such a Reidemeister graph is not of degree $2$, nor is it even regular, but I sense that the graph is sufficiently sparse that much of the exponential speedup would carry through.
