$
\def\dg{^\dagger}
\def\0{\bar0}
\def\1{\bar1}
\def\vk{\varphi_k}
\def\vl{\varphi_l}
\def\vm{\varphi_m}
\def\ket#1{\left\lvert#1\right\rangle}
\def\bra#1{\left\langle#1\right\rvert}
\def\braket#1#2{\left\langle#1\middle\vert#2\right\rangle}
\def\ketbra#1#2{\left\lvert#1\middle\rangle\!\middle\langle#2\right\rvert}
$
Resource
Section 3 in this lecture by Daniel Gottesman explains the Knill-Laflamme criterion with the 9-qubit Shor code as an example.
Breakdown of the Knill-Laflamme criteria
Simplification
$P_C$ is the projector onto the coding subspace $C$. If we have a code that protects 1-qubit information, we will have two states in our coding subspace representing logical zero $\ket\0$ and logical one $\ket\1$. As an example, in 3-qubit bit-flip code, $\ket\0 = \ket{000}$ and $\ket\1 = \ket{111}$. In such case, $P_C = \ketbra\0\0 + \ketbra\1\1$. Generally,
$$P_C = \sum_k\ketbra\vk\vk$$
where, $\ket\vk \in \text{basis}(C)$. So, an alternative way to represent the criteria:
\begin{align}
\sum_{kl} \ketbra\vk\vk E_i\dg E_j \ketbra\vl\vl
&= \alpha_{ij} \sum_m \ketbra\vm\vm
\\
\Rightarrow \bra\vk\left(
\sum_{kl}\ketbra\vk\vk E_i\dg E_j \ketbra\vl\vl
\right)\ket\vl
&= \alpha_{ij}\bra\vk\left(
\sum_m\ketbra\vm\vm
\right)\ket\vl
\\
\Rightarrow\bra\vk E_i\dg E_j\ket\vl
&= \alpha_{ij} \braket\vk\vl
= \alpha_{ij} \delta_{kl}
\end{align}
Preserve orthogonality between the transformed states
If we encounter an error, we should always be able to discern the transformed states. i.e. $E_i\ket\0$ should always be different from $E_i\ket\1$. Not only that, but different errors should also map the bases orthogonally: $\left(E_i\ket\0\right)\dg E_j\ket\1 = \bra\0E_i\dg E_j\ket\1 = 0$. Otherwise, we won't be able to discern which error took place.
Different errors map to different subspaces
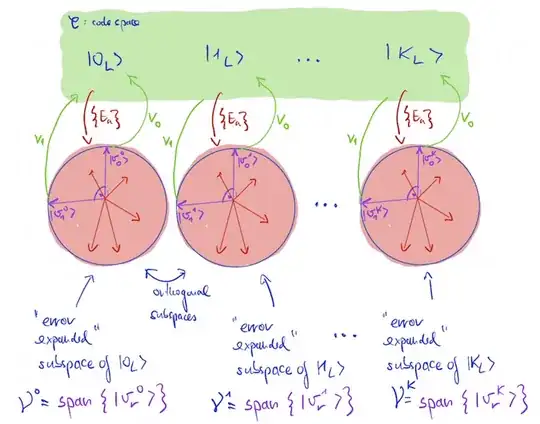
If any two different errors map coding subspace to different error subspaces (sufficient but not necessary), then the coding scheme fulfils the criteria: $\bra\vk E_i\dg E_j \ket\vk = 0 = \alpha_{ij}$. In such cases, we can easily detect which error took place.
But it is not necessary that different correctable errors should always map to different subspaces. This phenomenon is explained later.
Linear combination of correctable errors
If a code is able to correct a set of errors $\{E_i\}$, it should also be able to correct any linear combination of that error. For example, 3-qubit bit-flip code can correct errors with Kraus operators: $\left\{\sqrt{(1-p)^3}I, \sqrt{p(1-p)^2}X_1, \sqrt{p(1-p)^2}X_2, \sqrt{p(1-p)^2}X_3 \right\}$, where $p$ is the probability of single qubit bit-flip error. Any code that is able to correct $\{I, X_1, X_2, X_3\}$ will also be able to correct the above-mentioned set of operators since they are just scaled versions of each other.
Invariance of $\alpha_{ij}$ on basis
The linearity of correctable errors also shows why the $\alpha_{ij}$ is needed in the Knill-Laflamme criteria instead of just $\delta_{ij}$. For example, with $E_1 = \sqrt{p(1-p)^2}X_1$ we see that $\bra\0 E_1\dg E_1 \ket\0 = \bra\0 E_1\dg E_1 \ket\0 = p(1-p)^2 = \alpha_{11}$. Notice how the value of $\alpha_{ij}$ is only dependent on $i$ and $j$, but not the basis: $\bra\vk E_i\dg E_j\ket\vk = \alpha_{ij}$. Recall the fact that unitary operations preserve inner product. Here, the inner product of $E_i\ket\vk$ and $E_j\ket\vk$, $\bra\vk E_i\dg E_j \ket\vk$ remains constant whatever the $\ket\vk$ is. That means we can choose a different set of bases for the error, which might map errors to orthogonal subspaces.
A good example of this is $Z_1$ and $Z_2$ errors in 9-qubit Shor code. Both are correctable by the Shor code. Interestingly, $\bra\vk Z_1\dg Z_2 \ket\vk = 1$, meaning they are not orthogonal errors. But if we took a different basis $B_1 = \frac{Z_1+Z_2}{2}$ and $B_2 = \frac{Z_1 - Z_2}{2}$, we see that, $\bra\vk B_1\dg B_2 \ket\vk = \bra\vk (Z_1^2 - Z_2^2) \ket\vk = \bra\vk (I-I) \ket\vk = 0$, which are orthogonal. Both of these cases are handled well by the Knill-Laflamme criteria.
Hermitian operator $[\alpha_{ij}]$
The fact that $[\alpha_{ij}]$ is a Hermitian matrix can easily be shown by swapping indices $i$ and $j$ in the criteria equation: $\bra\vk E_i\dg E_j \ket\vk = \alpha_{ij} = \left(\bra\vk E_j\dg E_i \ket\vk\right)\dg = \left(\alpha_{ji}\right)\dg$.
One might falsely think different errors need to be mapped to different subspaces for them to be corrected, i.e. $\alpha_{ij} = 0$ is always true if $i \neq j$. Not necessarily. For example, 3-qubit bit-flip code can correct both $X_1$ error and $X_1 Z_2 Z_3$ error. Both of the errors map $\ket\0 = \ket{000}$ to $\ket{100}$ and $\ket\1 = \ket{111}$ to $\ket{011}$. So, which error has occurred is hardly of importance. What matters is the fact that both of them can be corrected by applying the $X_1$ operation. This is possible because both errors have identical effect on the coding subspace. This is reflected in the value of $\alpha_{ij}$: $\bra\vk E_i\dg E_j \ket\vk = \bra\vk X_1\dg X_1 Z_2 Z_3 \ket\vk = 1 = \alpha_{ij}$.