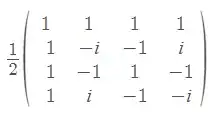I am not sure how to find the following matrix (the inverse of Quantum Fourier Transform) in terms of elementary quantum gates? I am using Qiskit to implement it.
Asked
Active
Viewed 539 times
1 Answers
2
Read the circuit for the QFT on 2 qubits and reverse and dagger everything
$$ (1 \otimes H)(Controlled(2,S_1^\dagger))(H \otimes 1) $$
Edit:
For how: Implementation of inverse QFT?
This decomposition is $m=2$ on https://en.wikipedia.org/wiki/Quantum_Fourier_transform Note that $R_2 = S$
$1 \otimes H$ to denote Hadamard on the second qubit. $H \otimes 1$ for Hadamard on the first. $Controlled(2,S_1^\dagger)$ for use qubit 2 as the control and assuming that apply $S^\dagger$ on the first qubit.
AHusain
- 3,723
- 2
- 11
- 18