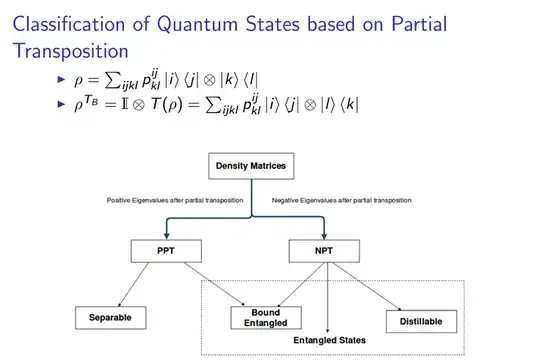
I'm going through some slides on the PPT/NPT criteria along with Horodecki's paper, and I'm kind of stuck. Let's take this slide:
Firstly, why can we write a bipartite density matrix as $\sum_{ijkl}\rho_{kl}^{ij}|i\rangle\langle j|\otimes |k\rangle\langle l|$? What states are the index labels $i, j, k, l$ referring to?
Secondly, Horodecki says on page 21 that if a $\rho_{AB}$ is separable then the new matrix $\rho_{AB}^{T_B}$ with matrix elements can be defined in some product basis as $\langle m|\langle \mu |\rho_{AB}^{T_B}|n\rangle|\nu\rangle = \langle m|\langle \nu|\rho_{AB}|n\rangle|\mu\rangle$. I don't quite understand where they're getting this form from. What are $|m\rangle, |n\rangle, |\mu\rangle, |\nu\rangle$?