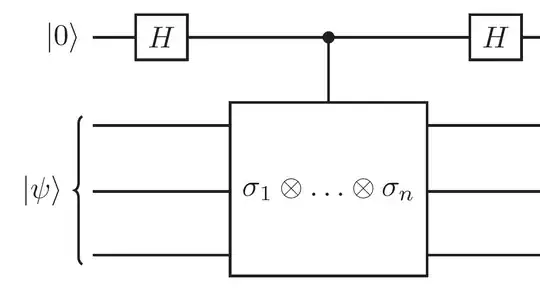
This may be a fairly basic question, but in Nielsen & Chuang, the following circuit is given for simulating $\exp\left(-i\Delta t Z_1 \otimes Z_2 \otimes Z_3\right)$: 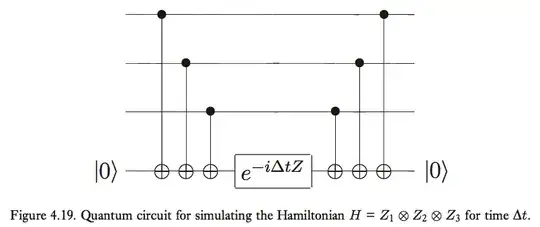
which uses an ancilla qubit initialized to $|0\rangle$. But from messing around with different gate sequences, it seems like this can be done with
\begin{align} CNOT_{1,2}CNOT_{1,3}e^{-i\Delta t Z_3}CNOT_{1,3}CNOT_{1,2} \end{align} or even \begin{align} CNOT_{1,2}CNOT_{2,3}e^{-i\Delta t Z_3}CNOT_{2,3}CNOT_{1,2} \end{align}
which doesn't require the ancilla and has two fewer CNOTs. Is there any advantage to using an ancilla qubit in this circuit?