Why should we use inverse QFT instead of QFT in Shor's algorithm? When I tried to simulate Shor's algorithm for small numbers, I got an answer even when I used just QFT instead of inverse QFT.
1 Answers
For Shor's algorithm, it actually doesn't matter which one you use.
If you apply the QFT twice, it is equivalent to a classical multiplication by -1 modulo $2^n$ where $n$ is the size of the register. That is to say, it reverses the order of all of the computational basis states except for $|0\rangle$ which stays where it started. $|k\rangle$ becomes $|-k\rangle = |2^n - k\rangle$.
Now, in Shor's algorithm, the output of the QFT is a state with amplitudes whose magnitudes are approximately periodic with a period that divides $2^n$. This isn't a coincidence; it's crucial to how the whole algorithm works. Because the period is a divisor of the number of computational basis states, reversing their order has a negligible effect on the state. Therefore there is little difference between using the QFT and the inverse QFT, because $\text{QFT}^{-1} = \text{QFT} \cdot \text{QFT}^{-1} \cdot \text{QFT}^{-1} = \text{QFT} \cdot \text{Mul}(-1)$.
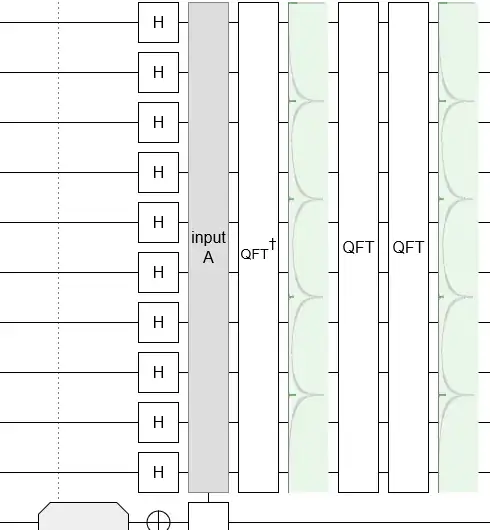
Note how the probability distributions are almost identical after an inverse QFT or after a QFT (in the above diagram the second qft is just to undo the inverse QFT). Since the output distribution is nearly identical the algorithm works either way.
- 44,299
- 1
- 41
- 116