Understanding the oracle in Deutsch's algorithm

Question

I am reading John Watrous' notes from his course CPSC 519 on quantum computing. In a pre-discussion before presenting Deutsch's algorithm to determine whether a function is constant or not, the author presents a function $B_f |x \rangle |y \rangle = |x \rangle |y \oplus f(x) \rangle $, and the diagram:

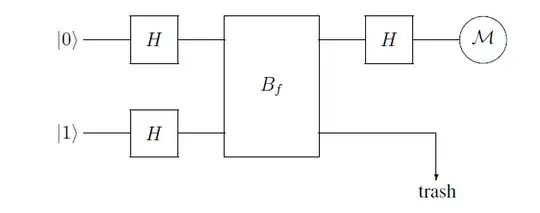
The inital state is $|0 \rangle |1 \rangle$, and after the first two Hadamard transforms, will be $$\big(\frac {1} {\sqrt 2} |0\rangle +\frac {1} {\sqrt 2} |1\rangle\big)\big(\frac {1} {\sqrt 2} |0\rangle-\frac {1} {\sqrt 2} |1\rangle\big) .$$

Up to this far I understand. The author then writes: "After performing the $B_f$ operation the state is transformed to:

$$\frac {1} {2} |0 \rangle \big(|0 \oplus f(0)\rangle - |1 \oplus f(0)\rangle\big) + \frac {1} {2} |1 \rangle \big(|0 \oplus f(1)\rangle) - |1 \oplus f(1) \rangle\big).$$

I am not sure how this was obtained, from what I understand, the operation should be $$\frac {1} {\sqrt 2} \big( |0\rangle + |1\rangle\big) \otimes \big|(\frac {1} {\sqrt 2} |0\rangle +\frac {1} {\sqrt 2} |1\rangle) \oplus f(\frac {1} {\sqrt 2} |0\rangle +\frac {1} {\sqrt 2} |1\rangle) \big\rangle$$ (simply subbing in $x,y$ to $B_f$). Any insights appreciated as this subject is completely new to me, although I have a decent mathematics and computer science background.

Answer 1

Remember that when you define the oracle effect as $B_f |x \rangle |y \rangle = |x \rangle |y \oplus f(x) \rangle $, $f(x)$ is a classical function of a classical 1-bit argument, so you do not have a way to compute $f(\frac {1} {\sqrt 2} |0\rangle +\frac {1} {\sqrt 2} |1\rangle)$ (a function of a quantum state).

The quantum oracles that implement classical functions are defined as follows:

1. Define the effect of the oracle on all basis states for $|x\rangle$ and $|y\rangle$: $B_f |x \rangle |y \rangle = |x \rangle |y \oplus f(x) \rangle $.

2. This will automatically define the effect of the oracle on all superposition states: the oracle is a quantum operation and has to be linear in the state on which it acts. So if you start with a state $\frac{1}{2} (|00\rangle + |10\rangle - |01\rangle - |11\rangle)$ (which is the state after applying Hadamard gates) and apply the oracle, you need to apply oracle to each basis state separately. You'll get

$$B_f \frac{1}{2} (|00\rangle + |10\rangle - |01\rangle - |11\rangle) = \frac{1}{2} (B_f|00\rangle + B_f|10\rangle - B_f|01\rangle - B_f|11\rangle) =$$

$$ = \frac{1}{2} (|0\rangle|0 \oplus f(0)\rangle + |1\rangle|0 \oplus f(1)\rangle - |0\rangle|1 \oplus f(0)\rangle - |1\rangle|1 \oplus f(1)\rangle)$$

Which is the same as the expression in the notes, up to a different grouping or terms.

---

The part about the oracles being defined by their effect on basis states is implicit in a lot of sources I've seen, and is a frequent source of confusion. If you need more mathematical details on this, we ended up writing it up here.