I have the following matrix
\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \frac{1}{\sqrt{2}} & \frac{-i}{\sqrt{2}} & 0\\ 0 & \frac{-i}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} I want to understand the operation by this matrix in terms of the familiar quantum logic gates. More precisely, how can one write the above matrix in terms of the quantum logic gates?
This gate, which I'll denote as $U$ is essentially the square root of not gate, whose decomposition has already been discussed elsewhere. Hence, we only need the conversion: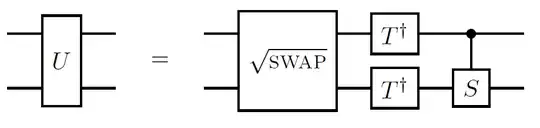
Specifically, if we perform the corresponding matrix multiplications, we have $$ \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & i \\ \end{array} \right)\cdot\left(\left( \begin{array}{cc} 1 & 0 \\ 0 & e^{-\frac{i \pi }{4}} \\ \end{array} \right)\otimes \left( \begin{array}{cc} 1 & 0 \\ 0 & e^{-\frac{i \pi }{4}} \\ \end{array} \right)\right)\cdot\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \frac{e^{\frac{i \pi }{4}}}{\sqrt{2}} & \frac{e^{-\frac{i \pi }{4}}}{\sqrt{2}} & 0 \\ 0 & \frac{e^{-\frac{i \pi }{4}}}{\sqrt{2}} & \frac{e^{\frac{i \pi }{4}}}{\sqrt{2}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right)=\\ \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & -\frac{i}{\sqrt{2}} & 0 \\ 0 & -\frac{i}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) $$ as required.
