How to construct a quantum circuit for the following state transformation?

Question

                      

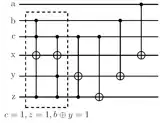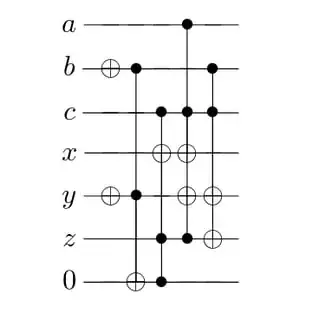
I have a certain transformations that goes as follows: Given $A=|abc\rangle$, $B=|xyz\rangle$, now I have cases as:

$$\text{if }c=1,z=1, b\oplus y=1 \implies \text{flip}(x)$$ $$\text{if }c=1, z=1 \implies \text{flip}(y)$$ $$\text{if }c=1\implies \text{flip}(z)$$ $$\text{if }b=1\implies \text{flip}(y)$$ $$\text{if }a=1\implies \text{flip}(x)$$

Can somebody just tell me the circuit for the bit-wise XOR that I have used between $b$ and $y$, i.e $b\oplus y=1$? The other gates I know are CNOT and Toffoli.

Answer 1

Why not simply try the following? You could have used an ancilla and computed $y\oplus b$ (that requires two controlled-nots, one controlled off each of $b$ and $y$, not a Toffoli) provided you later uncomputed the ancilla to reset it back to 0. But having an ancilla is unnecessary.

Just to explain what's happening in the boxed part of my circuit, both gates only work if $c=z=1$. Then the two gates flip $x$ depending on the value of $b$ or $y$ respectively. So, if $b\oplus y=1$, only one flip is applied, because one value is 0 and one value is 1. If $b\oplus y=0$, then either $b=y=0$, and no flip is applied, or $b=y=1$ and two flips are applied. But 2 flips cancel each other, so if $b\oplus y=0$, no operation is applied.