3

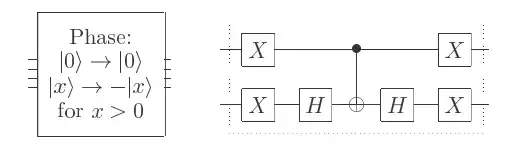
In the chapter about the Grover algorithm, it is suggested that the gate which executes the phase shift is given in the following form:

enter image description here

Now I have looked at this gate in detail and come to the conclusion that this "only" negates the state $|00\rangle$, but not all others, this can be shown for different inputs $|00\rangle$, $|01\rangle$, $|10\rangle$, $|11\rangle$ (the gate changes only $|00\rangle$ to -$|00\rangle$) or see here. I'm sorry, because in the chapter it says a few pages earlier: $|x\rangle$ becomes $-|x\rangle$ and $|0\rangle$ remains to $|0\rangle$ (picture left section). But that does not correspond to the circuit (picture right section). That's why I ask myself, what is right now? I want to do this a bit further, we say the Grover operator is:

$$H^{\otimes n}(2|0\rangle\langle 0|-I)H^{\otimes n}$$

That means I have several Hadamard transformations before and then do the phase shift, followed by Hadamard transformations. I think that you can see this in $(2|0\rangle\langle 0|-I)$ (matrix with 1 in the first row, all other rows -1), that $|x\rangle$ becomes $-|x\rangle$ and $|0\rangle$ stays $|0\rangle$. But that does not correspond to the circuit (picture right).

glS
  • 27,510
  • 7
  • 37
  • 125

1 Answers1

1

You are absolutely right. The picture in the right section correspond to the picture in the left section up to the unimportant global phase factor (-1). This fact mentioned in the Exercise 6.6.

The Box 6.1 use only one Grover iteration, so that $|ψ\rangle$ after this Grover iteration will be rotated to the (-$|x\rangle$) instead of $|x\rangle$ as in the general Grover algorithm. But this does not has any impact to the final result because the probability to find an $|x\rangle$ use the amplitude squire.

Alexey Krugovets
  • 160
  • 10