Why isn't the circuit performing a measurement in the Bell basis?

Question

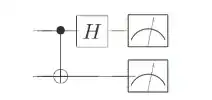
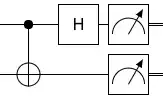
Nielsen and Chuang (on page 188 exercise 4.33) says that the circuit including CNOT and Hadamard is performing a measurement in the Bell basis. But I can't see how.

The matrix representing the circuit functionality is:

$$\begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & -1 \\ 0 & 1 &-1 & 0 \end{bmatrix}$$

Now, what I have found out is, that instead of measuring in the Bell state, it is actually simply converting $|00\rangle$ to $\beta_{00}$, $|01\rangle$ to $\beta_{01}$ and vice versa and so on. So it's actually transforming from one basis to another. But how is it a measurement in the Bell state?

Suppose you take the vector $(1,0,0,0)$ in the Bell state it's written $(1,0,1,0)$ then when measuring in Bell state I would expect you get either $(1,0,0,0)$ which is $|00\rangle + |11\rangle$ or $(0,0,1,0)$ which is $|00\rangle-|11\rangle$. But why isn't it doing the measurement but just converting from basis to basis and yet Wikipedia says it's a measurement?

Answer 1

1. You're correct that unitary gates like the Hadamard and CNOT do not perform any measurement. In fact, measurement isn't a unitary operation at all! There are separate measurements gates to measure the individual qubit states. The basis which the measurement gates will use is implementation dependent. However, in your specific circuit (N&C p. 188, Ex. 4.33) they're using the $\{|0\rangle, |1\rangle\}$ basis. Notice the meter type gates in your circuit. Those are the measurement gates. That circuit is essentially the one used to distinguish between the four orthogonal Bell states. They're mapped to $|00\rangle$, $|01\rangle$, $|10\rangle$ and $|11\rangle$ respectively. The mappings are (notations explained here):

$$|\Phi^+\rangle \to |00\rangle$$ $$|\Phi^-\rangle \to |10\rangle$$ $$|\Psi^+\rangle \to |01\rangle$$ $$|\Psi^-\rangle \to |11\rangle$$

2. As for how we can distinguish the four Bell states using two measurement gates, read Craig Gidney's answer to Distinguishing between orthogonal bell states.

Typically, a Bell basis measurement is done with a CNOT and a Hadamard like so:

It's exactly the reverse of making a Bell pair.

You can also simply do parity measurements along the X and Z axes:

---

Further Reading:

1. If all quantum gates must be unitary, what about measurement?

2. What does “measurement in a certain basis” mean?

3. How to measure relative phases of quantum states?

Answer 2

Just to supplement the given answer, if you want to know what the effective measurement is, you start from the measurement operators and work backwards. So, the two measurements mean that you're projecting on the states $|00\rangle,|01\rangle,|10\rangle,|11\rangle$. How do these transform under the preceding gates? Immediately before the measurement, we have a Hadamard on the first quibt. Incorporating that into the measurement basis means measuring in $|+0\rangle,|+1\rangle,|-0\rangle,|-1\rangle$. Finally, we incorporate the controlled-not, and we see that the overall thing corresponds to measurement in the Bell basis.